Hinweis

Zum Ende springen, um den vollständigen Beispielcode herunterzuladen.

Histogramm-Bins, Dichte und Gewicht#

Die Methode Axes.hist kann Histogramme auf verschiedene flexible Arten erstellen, was nützlich ist, aber auch zu Verwirrung führen kann. Insbesondere können Sie

  • die Daten nach Wunsch in Bins einteilen, entweder mit einer automatisch gewählten Anzahl von Bins oder mit festen Bin-Grenzen,

  • das Histogramm so normalisieren, dass sein Integral eins ergibt,

  • und den Datenpunkten Gewichte zuweisen, so dass jeder Datenpunkt die Zählung in seinem Bin unterschiedlich beeinflusst.

Die Matplotlib hist Methode ruft numpy.histogram auf und plottet die Ergebnisse. Daher sollten Benutzer die NumPy-Dokumentation für eine definitive Anleitung konsultieren.

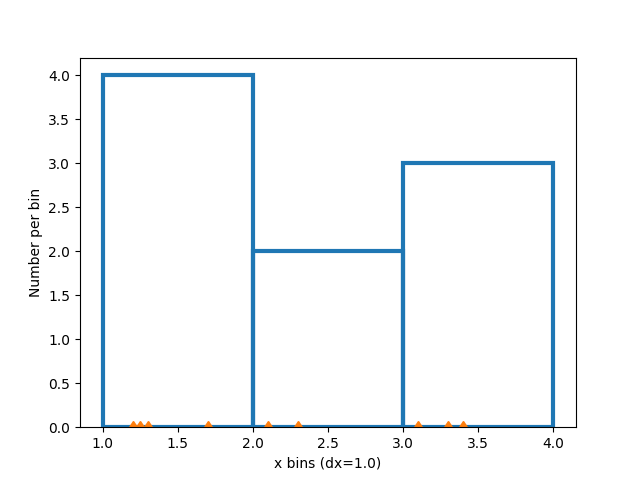
Histogramme werden erstellt, indem Bin-Grenzen definiert, ein Datensatz von Werten genommen und diese in die Bins sortiert werden, und dann gezählt oder summiert wird, wie viele Daten sich in jedem Bin befinden. In diesem einfachen Beispiel werden 9 Zahlen zwischen 1 und 4 in 3 Bins sortiert.

import matplotlib.pyplot as plt
import numpy as np

rng = np.random.default_rng(19680801)

xdata = np.array([1.2, 2.3, 3.3, 3.1, 1.7, 3.4, 2.1, 1.25, 1.3])
xbins = np.array([1, 2, 3, 4])

# changing the style of the histogram bars just to make it
# very clear where the boundaries of the bins are:
style = {'facecolor': 'none', 'edgecolor': 'C0', 'linewidth': 3}

fig, ax = plt.subplots()
ax.hist(xdata, bins=xbins, **style)

# plot the xdata locations on the x axis:
ax.plot(xdata, 0*xdata, 'd')
ax.set_ylabel('Number per bin')
ax.set_xlabel('x bins (dx=1.0)')
histogram normalization

Ändern von Bins#

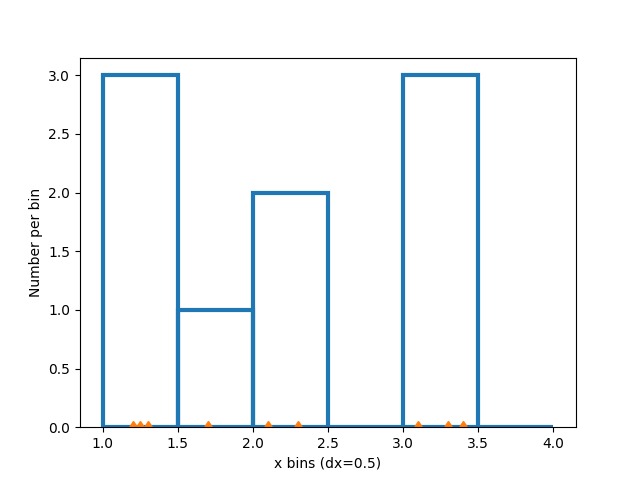
Das Ändern der Bin-Größe verändert die Form dieses spärlichen Histogramms, daher ist es ratsam, die Bins mit Bedacht in Bezug auf Ihre Daten zu wählen. Hier machen wir die Bins halb so breit.

xbins = np.arange(1, 4.5, 0.5)

fig, ax = plt.subplots()
ax.hist(xdata, bins=xbins, **style)
ax.plot(xdata, 0*xdata, 'd')
ax.set_ylabel('Number per bin')
ax.set_xlabel('x bins (dx=0.5)')
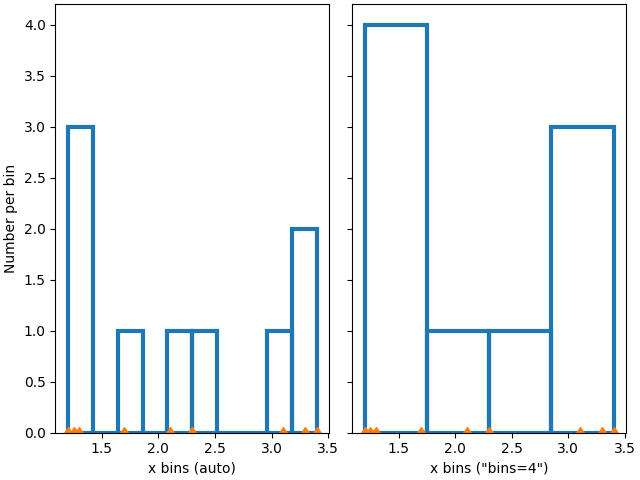
histogram normalization

Wir können NumPy (über Matplotlib) auch die Bins automatisch wählen lassen oder eine Anzahl von Bins angeben, die automatisch gewählt werden sollen.

fig, ax = plt.subplot_mosaic([['auto', 'n4']],
                             sharex=True, sharey=True, layout='constrained')

ax['auto'].hist(xdata, **style)
ax['auto'].plot(xdata, 0*xdata, 'd')
ax['auto'].set_ylabel('Number per bin')
ax['auto'].set_xlabel('x bins (auto)')

ax['n4'].hist(xdata, bins=4, **style)
ax['n4'].plot(xdata, 0*xdata, 'd')
ax['n4'].set_xlabel('x bins ("bins=4")')
histogram normalization

Normalisieren von Histogrammen: Dichte und Gewicht#

Anzahl pro Bin ist die Standardlänge jedes Balkens im Histogramm. Wir können jedoch auch die Balkenlängen als Wahrscheinlichkeitsdichtefunktion mit dem Parameter density normalisieren.

fig, ax = plt.subplots()
ax.hist(xdata, bins=xbins, density=True, **style)
ax.set_ylabel('Probability density [$V^{-1}$])')
ax.set_xlabel('x bins (dx=0.5 $V$)')
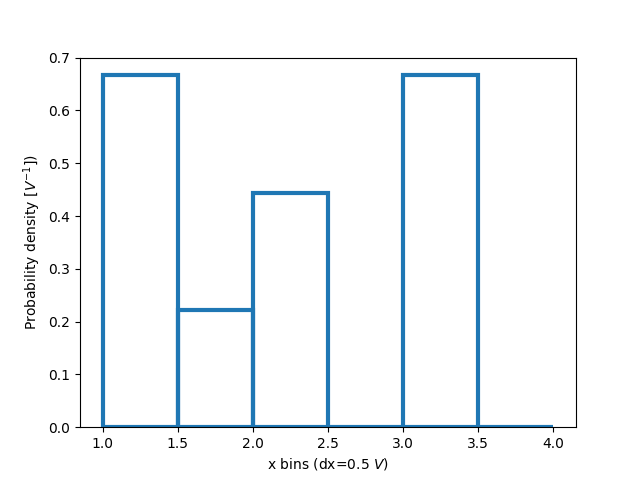
histogram normalization

Diese Normalisierung kann schwer zu interpretieren sein, wenn man nur die Daten erkundet. Der Wert, der jedem Balken zugeordnet ist, wird durch die Gesamtzahl der Datenpunkte *und* die Breite des Bins geteilt, und somit ergeben die Werte integriert eins, wenn man über den gesamten Datenbereich integriert. Z.B.

density = counts / (sum(counts) * np.diff(bins))
np.sum(density * np.diff(bins)) == 1

Diese Normalisierung ist, wie Wahrscheinlichkeitsdichtefunktionen in der Statistik definiert werden. Wenn \(X\) eine Zufallsvariable auf \(x\) ist, dann ist \(f_X\) die Wahrscheinlichkeitsdichtefunktion, wenn \(P[a<X<b] = \int_a^b f_X dx\). Wenn die Einheiten von x Volt sind, dann sind die Einheiten von \(f_X\) \(V^{-1}\) oder Wahrscheinlichkeit pro Spannungsänderung.

Der Nutzen dieser Normalisierung wird etwas klarer, wenn wir aus einer bekannten Verteilung ziehen und versuchen, mit der Theorie zu vergleichen. Wählen wir also 1000 Punkte aus einer Normalverteilung und berechnen wir auch die bekannte Wahrscheinlichkeitsdichtefunktion.

xdata = rng.normal(size=1000)
xpdf = np.arange(-4, 4, 0.1)
pdf = 1 / (np.sqrt(2 * np.pi)) * np.exp(-xpdf**2 / 2)

Wenn wir nicht density=True verwenden, müssen wir die erwartete Wahrscheinlichkeitsverteilungsfunktion sowohl mit der Länge der Daten als auch mit der Breite der Bins skalieren.

fig, ax = plt.subplot_mosaic([['False', 'True']], layout='constrained')
dx = 0.1
xbins = np.arange(-4, 4, dx)
ax['False'].hist(xdata, bins=xbins, density=False, histtype='step', label='Counts')

# scale and plot the expected pdf:
ax['False'].plot(xpdf, pdf * len(xdata) * dx, label=r'$N\,f_X(x)\,\delta x$')
ax['False'].set_ylabel('Count per bin')
ax['False'].set_xlabel('x bins [V]')
ax['False'].legend()

ax['True'].hist(xdata, bins=xbins, density=True, histtype='step', label='density')
ax['True'].plot(xpdf, pdf, label='$f_X(x)$')
ax['True'].set_ylabel('Probability density [$V^{-1}$]')
ax['True'].set_xlabel('x bins [$V$]')
ax['True'].legend()
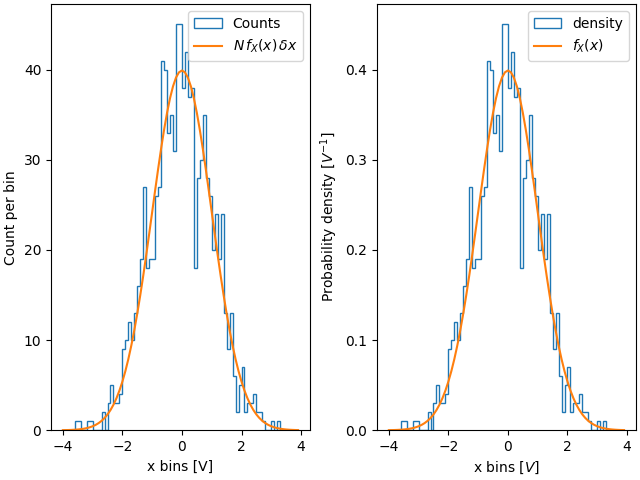
histogram normalization

Ein Vorteil der Dichte ist daher, dass die Form und Amplitude des Histogramms nicht von der Größe der Bins abhängt. Betrachten wir einen Extremfall, bei dem die Bins nicht die gleiche Breite haben. In diesem Beispiel sind die Bins unter x=-1.25 sechsmal breiter als die restlichen Bins. Durch die Normalisierung nach Dichte bewahren wir die Form der Verteilung, während bei Nicht-Normalisierung die breiteren Bins viel höhere Zählungen haben als die dünneren Bins.

fig, ax = plt.subplot_mosaic([['False', 'True']], layout='constrained')
dx = 0.1
xbins = np.hstack([np.arange(-4, -1.25, 6*dx), np.arange(-1.25, 4, dx)])
ax['False'].hist(xdata, bins=xbins, density=False, histtype='step', label='Counts')
ax['False'].plot(xpdf, pdf * len(xdata) * dx, label=r'$N\,f_X(x)\,\delta x_0$')
ax['False'].set_ylabel('Count per bin')
ax['False'].set_xlabel('x bins [V]')
ax['False'].legend()

ax['True'].hist(xdata, bins=xbins, density=True, histtype='step', label='density')
ax['True'].plot(xpdf, pdf, label='$f_X(x)$')
ax['True'].set_ylabel('Probability density [$V^{-1}$]')
ax['True'].set_xlabel('x bins [$V$]')
ax['True'].legend()
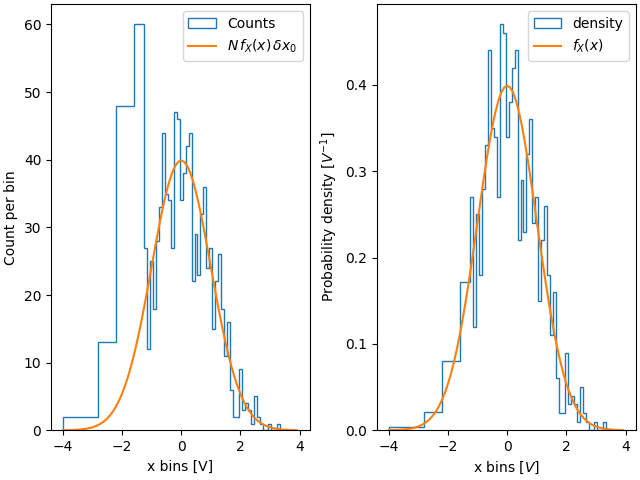
histogram normalization

Ebenso, wenn wir Histogramme mit unterschiedlichen Bin-Breiten vergleichen wollen, möchten wir vielleicht density=True verwenden.

fig, ax = plt.subplot_mosaic([['False', 'True']], layout='constrained')

# expected PDF
ax['True'].plot(xpdf, pdf, '--', label='$f_X(x)$', color='k')

for nn, dx in enumerate([0.1, 0.4, 1.2]):
    xbins = np.arange(-4, 4, dx)
    # expected histogram:
    ax['False'].plot(xpdf, pdf*1000*dx, '--', color=f'C{nn}')
    ax['False'].hist(xdata, bins=xbins, density=False, histtype='step')

    ax['True'].hist(xdata, bins=xbins, density=True, histtype='step', label=dx)

# Labels:
ax['False'].set_xlabel('x bins [$V$]')
ax['False'].set_ylabel('Count per bin')
ax['True'].set_ylabel('Probability density [$V^{-1}$]')
ax['True'].set_xlabel('x bins [$V$]')
ax['True'].legend(fontsize='small', title='bin width:')
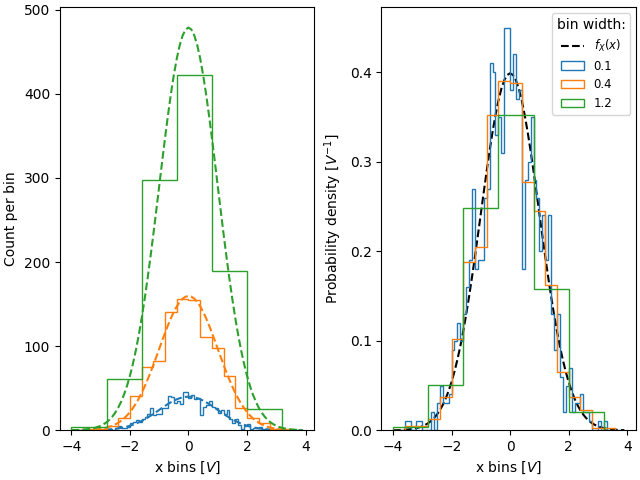
histogram normalization

Manchmal möchten die Leute so normalisieren, dass die Summe der Zählungen eins ergibt. Dies ist analog zu einer Wahrscheinlichkeitsmassenfunktion für eine diskrete Variable, bei der die Summe der Wahrscheinlichkeiten für alle Werte eins ergibt. Mit hist können wir diese Normalisierung erhalten, wenn wir die *Gewichte* auf 1/N setzen. Beachten Sie, dass die Amplitude dieses normalisierten Histogramms immer noch von der Breite und/oder Anzahl der Bins abhängt.

fig, ax = plt.subplots(layout='constrained', figsize=(3.5, 3))

for nn, dx in enumerate([0.1, 0.4, 1.2]):
    xbins = np.arange(-4, 4, dx)
    ax.hist(xdata, bins=xbins, weights=1/len(xdata) * np.ones(len(xdata)),
                   histtype='step', label=f'{dx}')
ax.set_xlabel('x bins [$V$]')
ax.set_ylabel('Bin count / N')
ax.legend(fontsize='small', title='bin width:')
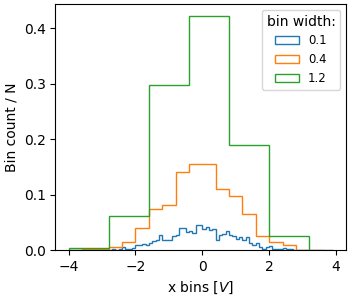
histogram normalization

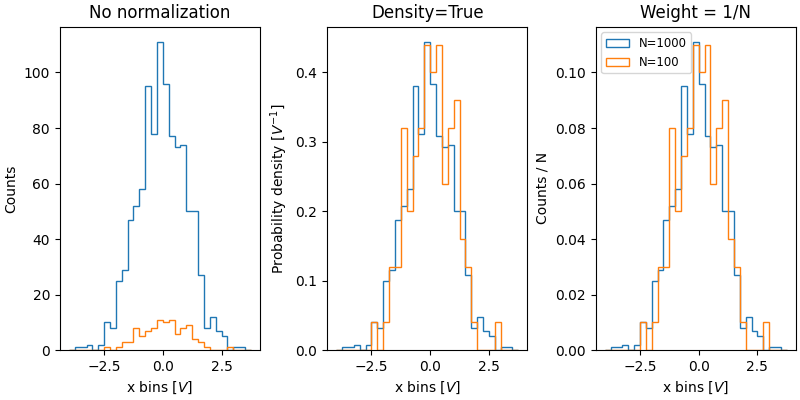
Der Wert der Normalisierung von Histogrammen liegt im Vergleich zweier Verteilungen, die unterschiedlich große Populationen haben. Hier vergleichen wir die Verteilung von xdata mit einer Population von 1000 und xdata2 mit 100 Mitgliedern.

xdata2 = rng.normal(size=100)

fig, ax = plt.subplot_mosaic([['no_norm', 'density', 'weight']],
                             layout='constrained', figsize=(8, 4))

xbins = np.arange(-4, 4, 0.25)

ax['no_norm'].hist(xdata, bins=xbins, histtype='step')
ax['no_norm'].hist(xdata2, bins=xbins, histtype='step')
ax['no_norm'].set_ylabel('Counts')
ax['no_norm'].set_xlabel('x bins [$V$]')
ax['no_norm'].set_title('No normalization')

ax['density'].hist(xdata, bins=xbins, histtype='step', density=True)
ax['density'].hist(xdata2, bins=xbins, histtype='step', density=True)
ax['density'].set_ylabel('Probability density [$V^{-1}$]')
ax['density'].set_title('Density=True')
ax['density'].set_xlabel('x bins [$V$]')

ax['weight'].hist(xdata, bins=xbins, histtype='step',
                  weights=1 / len(xdata) * np.ones(len(xdata)),
                  label='N=1000')
ax['weight'].hist(xdata2, bins=xbins, histtype='step',
                  weights=1 / len(xdata2) * np.ones(len(xdata2)),
                  label='N=100')
ax['weight'].set_xlabel('x bins [$V$]')
ax['weight'].set_ylabel('Counts / N')
ax['weight'].legend(fontsize='small')
ax['weight'].set_title('Weight = 1/N')

plt.show()
No normalization, Density=True, Weight = 1/N

Tags: plot-type: histogram domain: statistics

Referenzen

Die Verwendung der folgenden Funktionen, Methoden, Klassen und Module wird in diesem Beispiel gezeigt

Gesamtlaufzeit des Skripts: (0 Minuten 5,244 Sekunden)

Galerie generiert von Sphinx-Gallery

Auf dieser Seite