3D-Plot-Projektionstypen

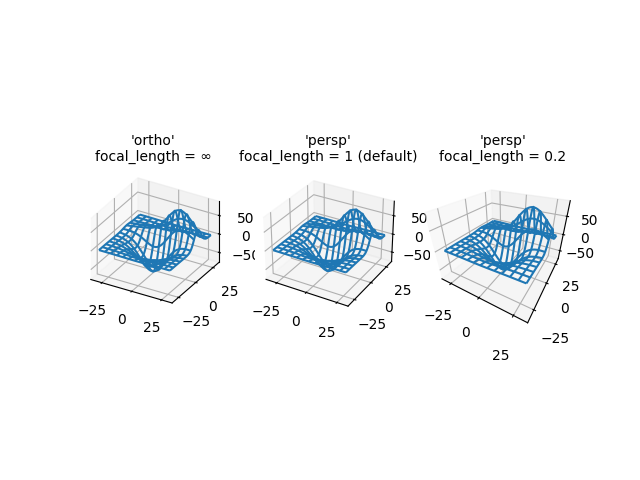
Demonstriert die verschiedenen Kamera-Projektionen für 3D-Plots und die Auswirkungen der Änderung der Brennweite für eine perspektivische Projektion. Beachten Sie, dass Matplotlib den "Zoom-Effekt" der Änderung der Brennweite korrigiert.

Die Standard-Brennweite von 1 entspricht einem Sichtfeld (FOV) von 90 Grad. Eine erhöhte Brennweite zwischen 1 und Unendlich "glättet" das Bild, während eine verringerte Brennweite zwischen 1 und 0 die Perspektive übertreibt und dem Bild mehr wahrnehmbare Tiefe verleiht. Im Grenzfall entspricht eine Brennweite von Unendlich einer orthografischen Projektion nach Korrektur des Zoom-Effekts.

Sie können die Brennweite über die Gleichung aus einem FOV berechnen

\[1 / \tan (\mathrm{FOV} / 2)\]

Oder umgekehrt

\[\mathrm{FOV} = 2 \arctan (1 / \mathrm{Brennweite})\]

import matplotlib.pyplot as plt

from mpl_toolkits.mplot3d import axes3d

fig, axs = plt.subplots(1, 3, subplot_kw={'projection': '3d'})

# Get the test data
X, Y, Z = axes3d.get_test_data(0.05)

# Plot the data
for ax in axs:
    ax.plot_wireframe(X, Y, Z, rstride=10, cstride=10)

# Set the orthographic projection.
axs[0].set_proj_type('ortho')  # FOV = 0 deg
axs[0].set_title("'ortho'\nfocal_length = ∞", fontsize=10)

# Set the perspective projections
axs[1].set_proj_type('persp')  # FOV = 90 deg
axs[1].set_title("'persp'\nfocal_length = 1 (default)", fontsize=10)

axs[2].set_proj_type('persp', focal_length=0.2)  # FOV = 157.4 deg
axs[2].set_title("'persp'\nfocal_length = 0.2", fontsize=10)

plt.show()

Tags: plot-type: 3D styling: small-multiples component: subplot level: intermediate