Hinweis
Gehe zum Ende, um den vollständigen Beispielcode herunterzuladen.
Verschachtelte Tortendiagramme#
Die folgenden Beispiele zeigen zwei Möglichkeiten, ein verschachteltes Tortendiagramm in Matplotlib zu erstellen. Solche Diagramme werden oft als Donut-Diagramme bezeichnet.
Siehe auch das Beispiel Linke Ventrikel-Bullseye.
import matplotlib.pyplot as plt
import numpy as np
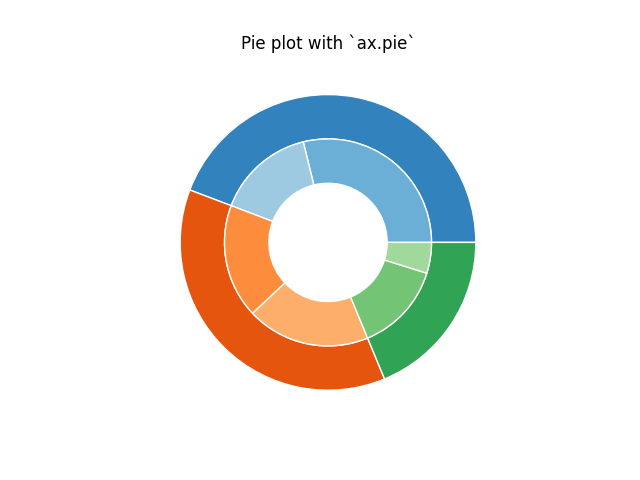
Der einfachste Weg, ein Tortendiagramm zu erstellen, ist die Verwendung der pie-Methode.
In diesem Fall nimmt `pie` Werte entgegen, die den Zählungen in einer Gruppe entsprechen. Wir werden zuerst einige fiktive Daten generieren, die drei Gruppen entsprechen. Im inneren Kreis behandeln wir jede Zahl als zu ihrer eigenen Gruppe gehörend. Im äußeren Kreis werden wir sie als Mitglieder ihrer ursprünglichen 3 Gruppen darstellen.
Der Effekt der Donut-Form wird durch Setzen einer width für die Keile des Tortendiagramms über das Argument wedgeprops erzielt.
fig, ax = plt.subplots()
size = 0.3
vals = np.array([[60., 32.], [37., 40.], [29., 10.]])
tab20c = plt.color_sequences["tab20c"]
outer_colors = [tab20c[i] for i in [0, 4, 8]]
inner_colors = [tab20c[i] for i in [1, 2, 5, 6, 9, 10]]
ax.pie(vals.sum(axis=1), radius=1, colors=outer_colors,
wedgeprops=dict(width=size, edgecolor='w'))
ax.pie(vals.flatten(), radius=1-size, colors=inner_colors,
wedgeprops=dict(width=size, edgecolor='w'))
ax.set(aspect="equal", title='Pie plot with `ax.pie`')
plt.show()
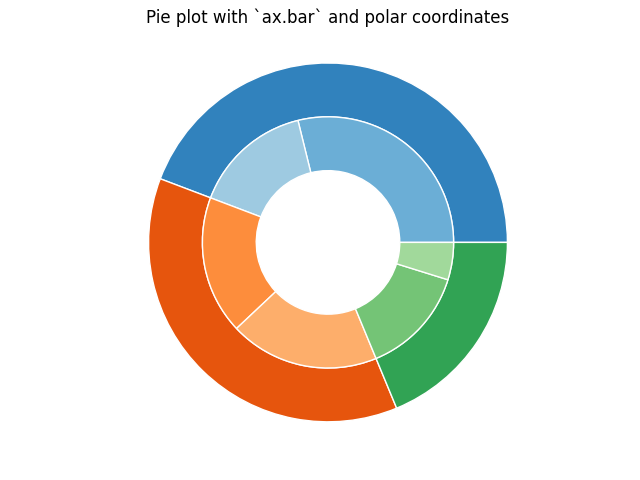
Sie können jedoch die gleiche Ausgabe erzielen, indem Sie ein Balkendiagramm auf `Axes` mit einem polaren Koordinatensystem verwenden. Dies kann mehr Flexibilität bei der genauen Gestaltung des Diagramms bieten.
In diesem Fall müssen wir die x-Werte des Balkendiagramms auf Radiane eines Kreises abbilden. Die kumulative Summe der Werte wird als Kanten der Balken verwendet.
fig, ax = plt.subplots(subplot_kw=dict(projection="polar"))
size = 0.3
vals = np.array([[60., 32.], [37., 40.], [29., 10.]])
# Normalize vals to 2 pi
valsnorm = vals/np.sum(vals)*2*np.pi
# Obtain the ordinates of the bar edges
valsleft = np.cumsum(np.append(0, valsnorm.flatten()[:-1])).reshape(vals.shape)
cmap = plt.colormaps["tab20c"]
outer_colors = cmap(np.arange(3)*4)
inner_colors = cmap([1, 2, 5, 6, 9, 10])
ax.bar(x=valsleft[:, 0],
width=valsnorm.sum(axis=1), bottom=1-size, height=size,
color=outer_colors, edgecolor='w', linewidth=1, align="edge")
ax.bar(x=valsleft.flatten(),
width=valsnorm.flatten(), bottom=1-2*size, height=size,
color=inner_colors, edgecolor='w', linewidth=1, align="edge")
ax.set(title="Pie plot with `ax.bar` and polar coordinates")
ax.set_axis_off()
plt.show()
Referenzen
Die Verwendung der folgenden Funktionen, Methoden, Klassen und Module wird in diesem Beispiel gezeigt