Zeitreihen-Histogramm#

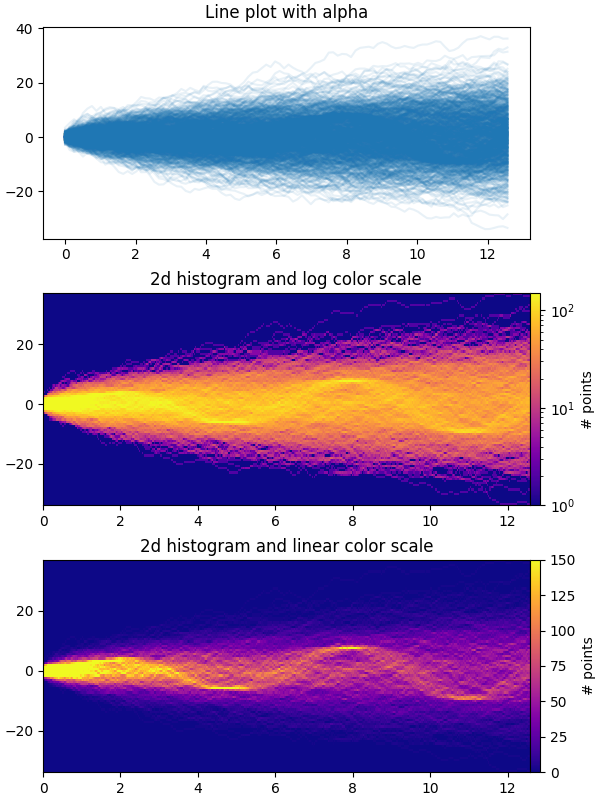
Dieses Beispiel demonstriert, wie große Mengen von Zeitreihen effizient visualisiert werden können, um potenziell verborgene Substrukturen und Muster aufzudecken, die nicht sofort ersichtlich sind, und sie visuell ansprechend darzustellen.

In diesem Beispiel generieren wir mehrere sinusförmige "Signal"-Reihen, die von einer größeren Anzahl von Zufallsbewegung ("Rausch-/Hintergrund"-Reihen) überlagert werden. Für eine unverzerrte Gaußsche Zufallsbewegung mit einer Standardabweichung von σ beträgt die RMS-Abweichung vom Ursprung nach n Schritten σ*sqrt(n). Um die Sinuskurven auf derselben Skala wie die Zufallsbewegungen sichtbar zu halten, skalieren wir die Amplitude mit der RMS der Zufallsbewegung. Zusätzlich führen wir einen kleinen zufälligen Offset phi ein, um die Sinuskurven nach links/rechts zu verschieben, und fügen etwas additives zufälliges Rauschen hinzu, um einzelne Datenpunkte nach oben/unten zu verschieben, damit das Signal etwas "realistischer" wird (man würde nicht erwarten, dass eine perfekte Sinuswelle in seinen Daten auftaucht).

Das erste Diagramm zeigt die typische Methode zur Visualisierung mehrerer Zeitreihen, indem sie mit plt.plot und einem kleinen Wert für alpha übereinandergelegt werden. Das zweite und dritte Diagramm zeigen, wie die Daten als 2D-Histogramm mit optionaler Interpolation zwischen den Datenpunkten neu interpretiert werden können, indem np.histogram2d und plt.pcolormesh verwendet werden.

import time

import matplotlib.pyplot as plt
import numpy as np

fig, axes = plt.subplots(nrows=3, figsize=(6, 8), layout='constrained')

# Fix random state for reproducibility
np.random.seed(19680801)
# Make some data; a 1D random walk + small fraction of sine waves
num_series = 1000
num_points = 100
SNR = 0.10  # Signal to Noise Ratio
x = np.linspace(0, 4 * np.pi, num_points)
# Generate unbiased Gaussian random walks
Y = np.cumsum(np.random.randn(num_series, num_points), axis=-1)
# Generate sinusoidal signals
num_signal = round(SNR * num_series)
phi = (np.pi / 8) * np.random.randn(num_signal, 1)  # small random offset
Y[-num_signal:] = (
    np.sqrt(np.arange(num_points))  # random walk RMS scaling factor
    * (np.sin(x - phi)
       + 0.05 * np.random.randn(num_signal, num_points))  # small random noise
)


# Plot series using `plot` and a small value of `alpha`. With this view it is
# very difficult to observe the sinusoidal behavior because of how many
# overlapping series there are. It also takes a bit of time to run because so
# many individual artists need to be generated.
tic = time.time()
axes[0].plot(x, Y.T, color="C0", alpha=0.1)
toc = time.time()
axes[0].set_title("Line plot with alpha")
print(f"{toc-tic:.3f} sec. elapsed")


# Now we will convert the multiple time series into a histogram. Not only will
# the hidden signal be more visible, but it is also a much quicker procedure.
tic = time.time()
# Linearly interpolate between the points in each time series
num_fine = 800
x_fine = np.linspace(x.min(), x.max(), num_fine)
y_fine = np.concatenate([np.interp(x_fine, x, y_row) for y_row in Y])
x_fine = np.broadcast_to(x_fine, (num_series, num_fine)).ravel()


# Plot (x, y) points in 2d histogram with log colorscale
# It is pretty evident that there is some kind of structure under the noise
# You can tune vmax to make signal more visible
cmap = plt.colormaps["plasma"]
cmap = cmap.with_extremes(bad=cmap(0))
h, xedges, yedges = np.histogram2d(x_fine, y_fine, bins=[400, 100])
pcm = axes[1].pcolormesh(xedges, yedges, h.T, cmap=cmap,
                         norm="log", vmax=1.5e2, rasterized=True)
fig.colorbar(pcm, ax=axes[1], label="# points", pad=0)
axes[1].set_title("2d histogram and log color scale")

# Same data but on linear color scale
pcm = axes[2].pcolormesh(xedges, yedges, h.T, cmap=cmap,
                         vmax=1.5e2, rasterized=True)
fig.colorbar(pcm, ax=axes[2], label="# points", pad=0)
axes[2].set_title("2d histogram and linear color scale")

toc = time.time()
print(f"{toc-tic:.3f} sec. elapsed")
plt.show()

Line plot with alpha, 2d histogram and log color scale, 2d histogram and linear color scale

0.344 sec. elapsed
0.131 sec. elapsed

Tags: plot-type: histogram2d plot-type: pcolormesh purpose: storytelling styling: color component: colormap

Referenzen

Die Verwendung der folgenden Funktionen, Methoden, Klassen und Module wird in diesem Beispiel gezeigt

Gesamtlaufzeit des Skripts: (0 Minuten 3,025 Sekunden)

Galerie generiert von Sphinx-Gallery