pcolormesh#

axes.Axes.pcolormesh ermöglicht Ihnen die Erstellung von 2D-bildähnlichen Diagrammen. Beachten Sie, dass es schneller ist als das ähnliche pcolor.

import matplotlib.pyplot as plt
import numpy as np

from matplotlib.colors import BoundaryNorm
from matplotlib.ticker import MaxNLocator

Grundlegendes pcolormesh#

Wir definieren ein pcolormesh normalerweise, indem wir die Kanten von Vierecken und den Wert des Vierecks angeben. Beachten Sie, dass x und y hier jeweils ein Element mehr als Z in der jeweiligen Dimension haben.

np.random.seed(19680801)
Z = np.random.rand(6, 10)
x = np.arange(-0.5, 10, 1)  # len = 11
y = np.arange(4.5, 11, 1)  # len = 7

fig, ax = plt.subplots()
ax.pcolormesh(x, y, Z)

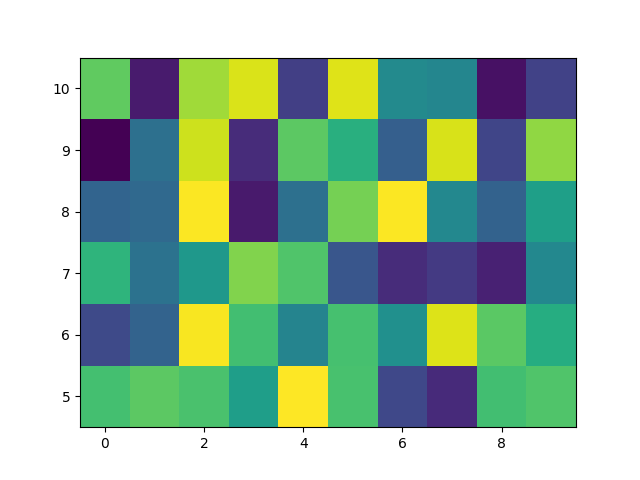
Nicht-geradliniges pcolormesh#

Beachten Sie, dass wir auch Matrizen für X und Y angeben und nicht-geradlinige Vierecke haben können.

x = np.arange(-0.5, 10, 1)  # len = 11
y = np.arange(4.5, 11, 1)  # len = 7
X, Y = np.meshgrid(x, y)
X = X + 0.2 * Y  # tilt the coordinates.
Y = Y + 0.3 * X

fig, ax = plt.subplots()
ax.pcolormesh(X, Y, Z)

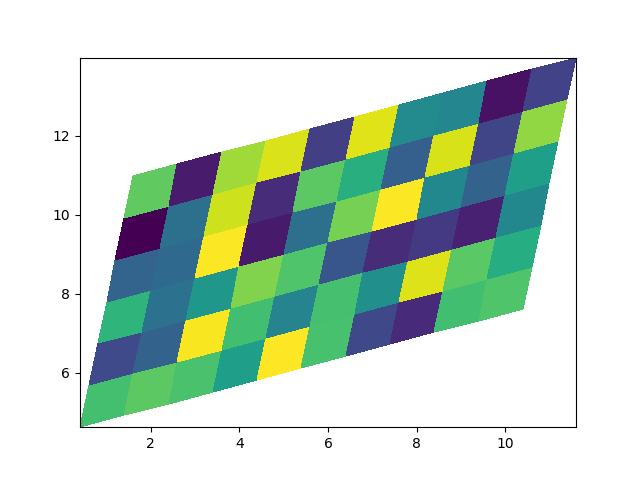
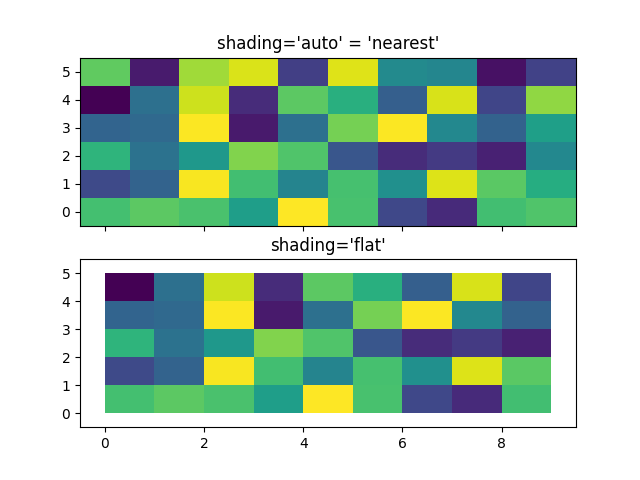
Zentrierte Koordinaten#

Oft möchte ein Benutzer X und Y mit denselben Größen wie Z an axes.Axes.pcolormesh übergeben. Dies ist auch zulässig, wenn shading='auto' übergeben wird (standardmäßig gesetzt durch rcParams["pcolor.shading"] (Standard: 'auto')). Vor Matplotlib 3.3 hat shading='flat' die letzte Spalte und Zeile von Z fallen gelassen, gibt jetzt aber einen Fehler aus. Wenn dies wirklich das ist, was Sie wollen, dann lassen Sie einfach die letzte Zeile und Spalte von Z manuell fallen.

x = np.arange(10)  # len = 10
y = np.arange(6)  # len = 6
X, Y = np.meshgrid(x, y)

fig, axs = plt.subplots(2, 1, sharex=True, sharey=True)
axs[0].pcolormesh(X, Y, Z, vmin=np.min(Z), vmax=np.max(Z), shading='auto')
axs[0].set_title("shading='auto' = 'nearest'")
axs[1].pcolormesh(X, Y, Z[:-1, :-1], vmin=np.min(Z), vmax=np.max(Z),
                  shading='flat')
axs[1].set_title("shading='flat'")

shading='auto' = 'nearest', shading='flat'

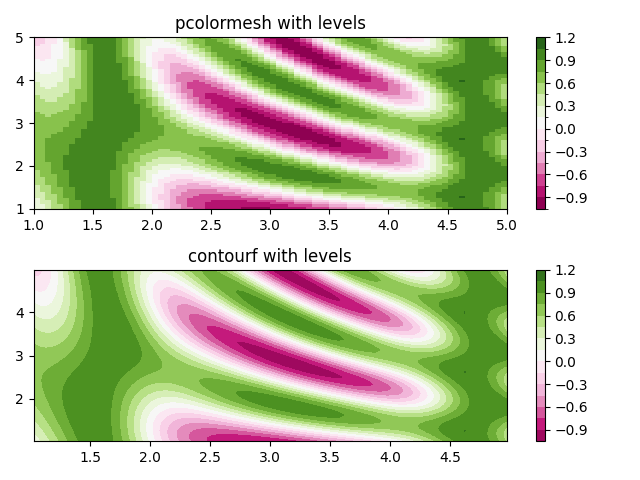
Ebenen mit Normen erstellen#

Zeigt, wie Normalisierungs- und Colormap-Instanzen kombiniert werden können, um "Ebenen" in axes.Axes.pcolor, axes.Axes.pcolormesh und axes.Axes.imshow-Typ-Diagrammen auf ähnliche Weise wie das `levels`-Schlüsselwortargument für `contour`/`contourf` zu zeichnen.

# make these smaller to increase the resolution
dx, dy = 0.05, 0.05

# generate 2 2d grids for the x & y bounds
y, x = np.mgrid[slice(1, 5 + dy, dy),
                slice(1, 5 + dx, dx)]

z = np.sin(x)**10 + np.cos(10 + y*x) * np.cos(x)

# x and y are bounds, so z should be the value *inside* those bounds.
# Therefore, remove the last value from the z array.
z = z[:-1, :-1]
levels = MaxNLocator(nbins=15).tick_values(z.min(), z.max())


# pick the desired colormap, sensible levels, and define a normalization
# instance which takes data values and translates those into levels.
cmap = plt.colormaps['PiYG']
norm = BoundaryNorm(levels, ncolors=cmap.N, clip=True)

fig, (ax0, ax1) = plt.subplots(nrows=2)

im = ax0.pcolormesh(x, y, z, cmap=cmap, norm=norm)
fig.colorbar(im, ax=ax0)
ax0.set_title('pcolormesh with levels')


# contours are *point* based plots, so convert our bound into point
# centers
cf = ax1.contourf(x[:-1, :-1] + dx/2.,
                  y[:-1, :-1] + dy/2., z, levels=levels,
                  cmap=cmap)
fig.colorbar(cf, ax=ax1)
ax1.set_title('contourf with levels')

# adjust spacing between subplots so `ax1` title and `ax0` tick labels
# don't overlap
fig.tight_layout()

plt.show()

pcolormesh with levels, contourf with levels

Referenzen

Die Verwendung der folgenden Funktionen, Methoden, Klassen und Module wird in diesem Beispiel gezeigt

Gesamtlaufzeit des Skripts: (0 Minuten 3,551 Sekunden)

Galerie generiert von Sphinx-Gallery