Logarithmische Skala

Beispiele für Diagramme mit logarithmischen Achsen.

Sie können die x/y-Achsen logarithmisch einstellen, indem Sie "log" an set_xscale / set_yscale übergeben.

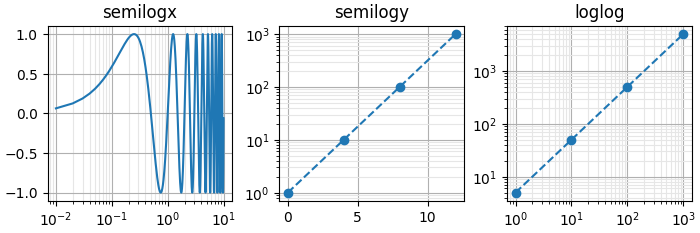
Bequemlichkeitsfunktionen semilogx, semilogy und loglog

Da das Plotten von Daten auf semi-logarithmischen oder doppel-logarithmischen Skalen sehr üblich ist, sind die Funktionen semilogx, semilogy und loglog Abkürzungen zum Einstellen der Skala und zum Plotten von Daten; z.B. ist ax.semilogx(x, y) äquivalent zu ax.set_xscale('log'); ax.plot(x, y).

import matplotlib.pyplot as plt
import numpy as np

fig, (ax1, ax2, ax3) = plt.subplots(1, 3, layout='constrained', figsize=(7, 7/3))
# log x axis
t = np.arange(0.01, 10.0, 0.01)
ax1.semilogx(t, np.sin(2 * np.pi * t))
ax1.set(title='semilogx')
ax1.grid()
ax1.grid(which="minor", color="0.9")

# log y axis
x = np.arange(4)
ax2.semilogy(4*x, 10**x, 'o--')
ax2.set(title='semilogy')
ax2.grid()
ax2.grid(which="minor", color="0.9")

# log x and y axis
x = np.array([1, 10, 100, 1000])
ax3.loglog(x, 5 * x, 'o--')
ax3.set(title='loglog')
ax3.grid()
ax3.grid(which="minor", color="0.9")

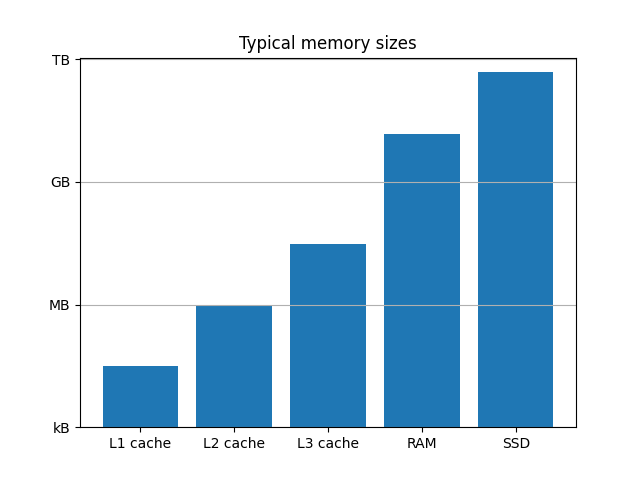
Logarithmen mit anderen Basen

Standardmäßig ist die logarithmische Skala zur Basis 10. Dies kann über den Parameter base geändert werden.

fig, ax = plt.subplots()
ax.bar(["L1 cache", "L2 cache", "L3 cache", "RAM", "SSD"],
       [32, 1_000, 32_000, 16_000_000, 512_000_000])
ax.set_yscale('log', base=2)
ax.set_yticks([1, 2**10, 2**20, 2**30], labels=['kB', 'MB', 'GB', 'TB'])
ax.set_title("Typical memory sizes")
ax.yaxis.grid()

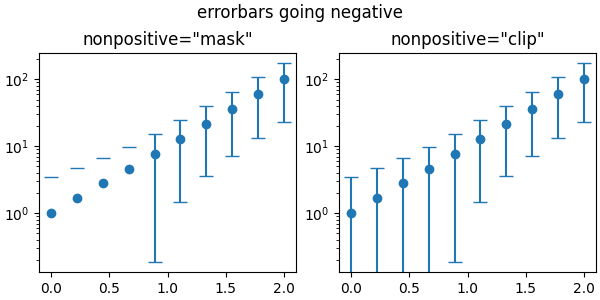
Umgang mit negativen Werten

Nicht-positive Werte können auf einer logarithmischen Skala nicht dargestellt werden. Die Skala hat zwei Optionen, um damit umzugehen. Entweder werden die Werte maskiert, so dass sie ignoriert werden, oder sie werden auf einen kleinen positiven Wert abgeschnitten. Welche Option besser geeignet ist, hängt von der Art der Daten und der Visualisierung ab.

Das folgende Beispiel enthält Fehlermarkierungen, die negativ sind. Wenn wir diese Werte maskieren, verschwindet die Markierung, was nicht wünschenswert ist. Im Gegensatz dazu schneidet das Abschneiden den Wert auf einen kleinen positiven Wert (aber weit unterhalb der verwendeten Skala) ab, so dass die Fehlermarkierung bis zum Rand der Achse gezeichnet wird.

x = np.linspace(0.0, 2.0, 10)
y = 10**x
yerr = 1.75 + 0.75*y

fig, (ax1, ax2) = plt.subplots(1, 2, layout="constrained", figsize=(6, 3))
fig.suptitle("errorbars going negative")
ax1.set_yscale("log", nonpositive='mask')
ax1.set_title('nonpositive="mask"')
ax1.errorbar(x, y, yerr=yerr, fmt='o', capsize=5)

ax2.set_yscale("log", nonpositive='clip')
ax2.set_title('nonpositive="clip"')
ax2.errorbar(x, y, yerr=yerr, fmt='o', capsize=5)

plt.show()