Symlog-Skala

Die symmetrische logarithmische Skala ist eine Erweiterung der logarithmischen Skala, die auch negative Werte abdeckt. Wie bei der logarithmischen Skala ist sie besonders nützlich für numerische Daten, die einen großen Wertebereich umfassen, insbesondere wenn es signifikante Unterschiede zwischen den Größenordnungen der beteiligten Zahlen gibt.

Beispielhafte Verwendung der symlog-Achsenskalierung (symmetrisch logarithmisch).

import matplotlib.pyplot as plt
import numpy as np

dt = 0.01
x = np.arange(-50.0, 50.0, dt)
y = np.arange(0, 100.0, dt)

fig, (ax0, ax1, ax2) = plt.subplots(nrows=3)

ax0.plot(x, y)
ax0.set_xscale('symlog')
ax0.set_ylabel('symlogx')
ax0.grid()
ax0.xaxis.grid(which='minor')  # minor grid on too

ax1.plot(y, x)
ax1.set_yscale('symlog')
ax1.set_ylabel('symlogy')

ax2.plot(x, np.sin(x / 3.0))
ax2.set_xscale('symlog')
ax2.set_yscale('symlog', linthresh=0.015)
ax2.grid()
ax2.set_ylabel('symlog both')

fig.tight_layout()
plt.show()

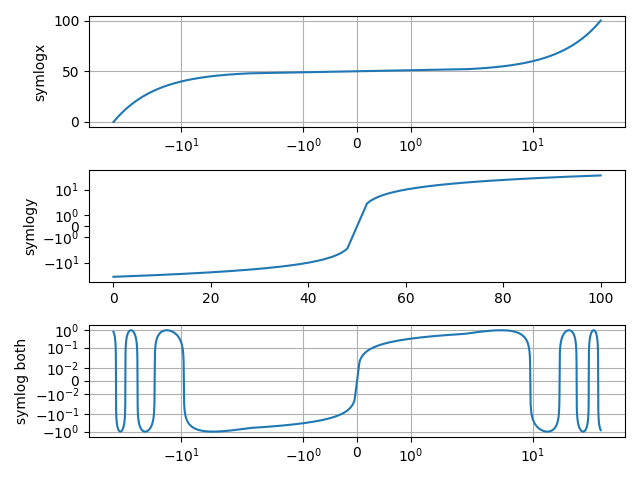
Lineare Schwelle

Da jede Dekade auf einer logarithmischen Skala den gleichen visuellen Raum einnimmt und es unendlich viele Dekaden zwischen einer gegebenen Zahl und Null gibt, muss die symlog-Skala in einem kleinen Bereich (-linthresh, linthresh) vom logarithmischen Mapping abweichen, damit der Bereich auf einen endlichen visuellen Raum abgebildet wird.

def format_axes(ax, title=None):
    """A helper function to better visualize properties of the symlog scale."""
    ax.xaxis.get_minor_locator().set_params(subs=[2, 3, 4, 5, 6, 7, 8, 9])
    ax.grid()
    ax.xaxis.grid(which='minor')  # minor grid on too
    linthresh = ax.xaxis.get_transform().linthresh
    linscale = ax.xaxis.get_transform().linscale
    ax.axvspan(-linthresh, linthresh, color='0.9')
    if title:
        ax.set_title(title.format(linthresh=linthresh, linscale=linscale))


x = np.linspace(-60, 60, 201)
y = np.linspace(0, 100.0, 201)

fig, (ax1, ax2) = plt.subplots(nrows=2, layout="constrained")

ax1.plot(x, y)
ax1.set_xscale('symlog', linthresh=1)
format_axes(ax1, title='Linear region: linthresh={linthresh}')

ax2.plot(x, y)
ax2.set_xscale('symlog', linthresh=5)
format_axes(ax2, title='Linear region: linthresh={linthresh}')

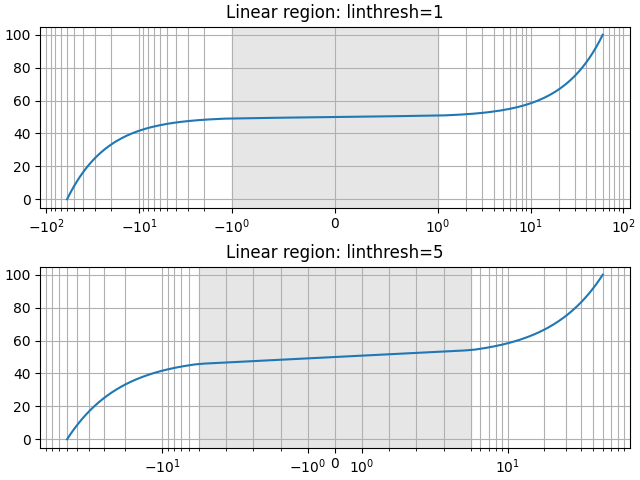
Im Allgemeinen sollte linthresh so gewählt werden, dass keine oder nur wenige Datenpunkte im linearen Bereich liegen. Als Faustregel gilt: \(linthresh \approx \mathrm{min} |x|\).

Lineare Skala

Zusätzlich bestimmt der Parameter linscale, wie viel visueller Raum für den linearen Bereich verwendet werden soll. Genauer gesagt definiert er das Verhältnis des visuellen Raums des Bereichs (0, linthresh) im Verhältnis zu einer Dekade.

fig, (ax1, ax2) = plt.subplots(nrows=2, layout="constrained")

ax1.plot(x, y)
ax1.set_xscale('symlog', linthresh=1)
format_axes(ax1, title='Linear region: linthresh={linthresh}, linscale={linscale}')

ax2.plot(x, y)
ax2.set_xscale('symlog', linthresh=1, linscale=0.1)
format_axes(ax2, title='Linear region: linthresh={linthresh}, linscale={linscale}')

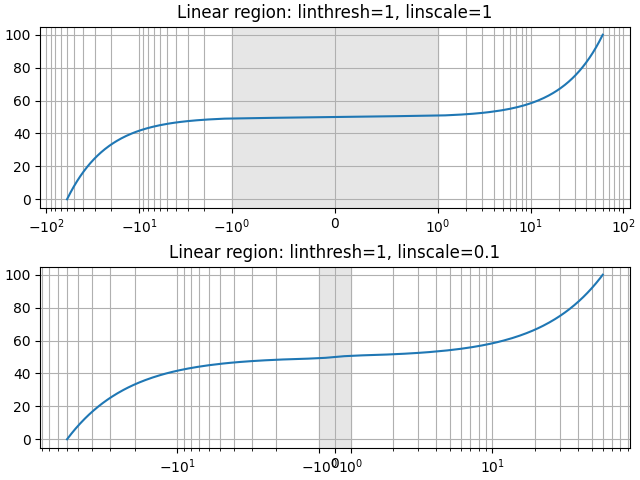
Der geeignete Wert für linscale hängt vom dynamischen Bereich der Daten ab. Da die meisten Daten außerhalb des linearen Bereichs liegen werden, verwenden Sie typischerweise den linearen Bereich nur, um einen kleinen Teil der visuellen Fläche abzudecken.

Einschränkungen und Alternativen

Die von symlog verwendete Koordinatentransformation weist an der Übergangsstelle zwischen ihren linearen und logarithmischen Bereichen einen diskontinuierlichen Gradienten auf. Je nach Daten und Skalierung wird dies im Plot mehr oder weniger offensichtlich sein.

fig, ax = plt.subplots()
ax.plot(x, y)
ax.set_xscale('symlog', linscale=0.05)
format_axes(ax, title="Discontinuous gradient at linear/log transition")

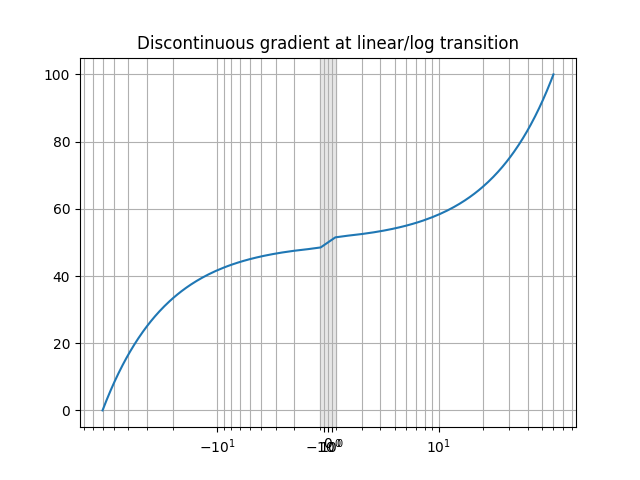
Die asinh Achsenskala ist eine alternative Transformation, die einen großen dynamischen Bereich mit einem glatten Gradienten unterstützt und daher solche visuellen Artefakte vermeiden kann. Siehe Asinh-Skala.

Referenzen

• matplotlib.scale.SymmetricalLogScale

• matplotlib.ticker.SymmetricalLogLocator

• matplotlib.scale.AsinhScale