Achsenkastenverhältnis

Diese Demo zeigt, wie das Verhältnis eines Achsenkastens direkt über set_box_aspect eingestellt werden kann. Das Kastenverhältnis ist das Verhältnis zwischen Achsenhöhe und Achsenbreite in physikalischen Einheiten, unabhängig von den Datenlimits. Dies ist nützlich, um z. B. ein quadratisches Diagramm zu erstellen, unabhängig von den enthaltenen Daten, oder um neben einem Bilddiagramm mit festem (Daten-)Verhältnis ein normales Diagramm mit denselben Achsendimensionen zu haben.

Die folgende Liste enthält einige Anwendungsfälle für set_box_aspect.

Eine quadratische Achse, unabhängig von den Daten

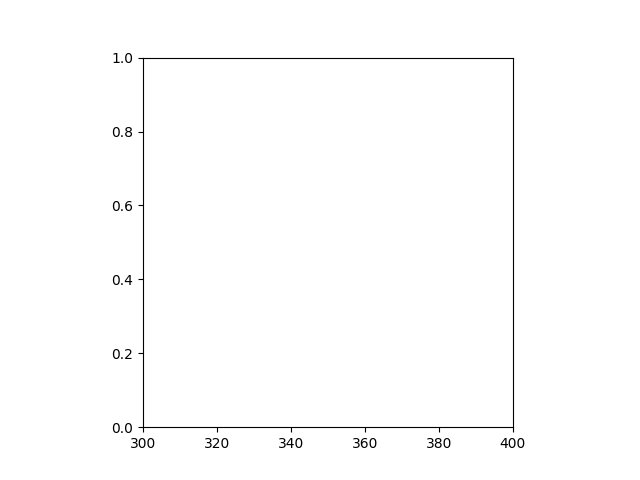
Erzeugt eine quadratische Achse, unabhängig von den Datenlimits.

import matplotlib.pyplot as plt
import numpy as np

fig1, ax = plt.subplots()

ax.set_xlim(300, 400)
ax.set_box_aspect(1)

plt.show()

Gemeinsame quadratische Achsen

Erzeugt gemeinsame Unterdiagramme, die quadratisch in der Größe sind.

fig2, (ax, ax2) = plt.subplots(ncols=2, sharey=True)

ax.plot([1, 5], [0, 10])
ax2.plot([100, 500], [10, 15])

ax.set_box_aspect(1)
ax2.set_box_aspect(1)

plt.show()

Quadratische Zwillingsachsen

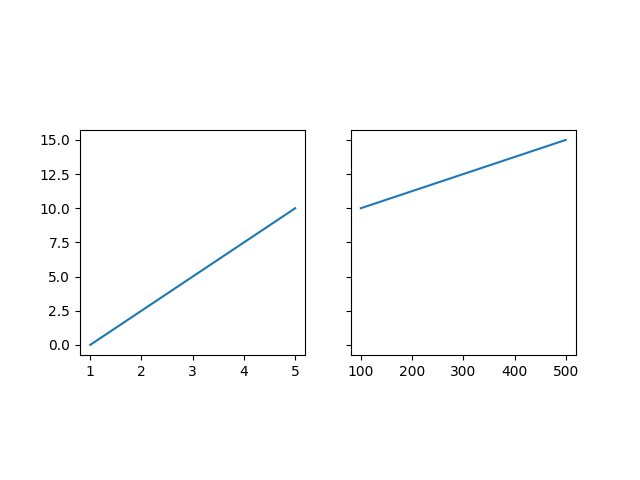
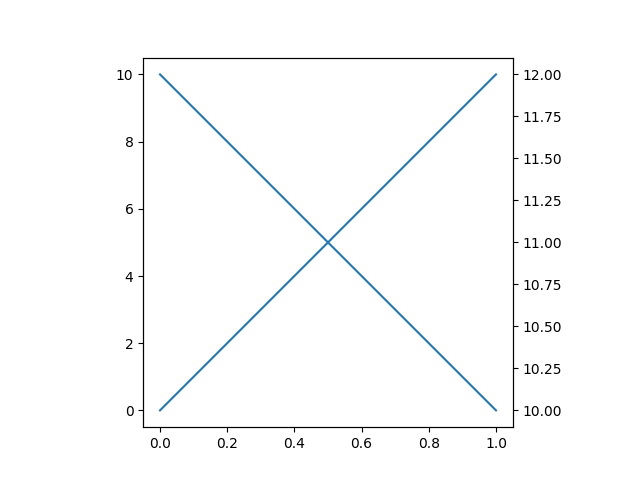
Erzeugt eine quadratische Achse mit einer Zwillingsachse. Die Zwillingsachse übernimmt das Kastenverhältnis der Elternachse.

fig3, ax = plt.subplots()

ax2 = ax.twinx()

ax.plot([0, 10])
ax2.plot([12, 10])

ax.set_box_aspect(1)

plt.show()

Normales Diagramm neben Bild

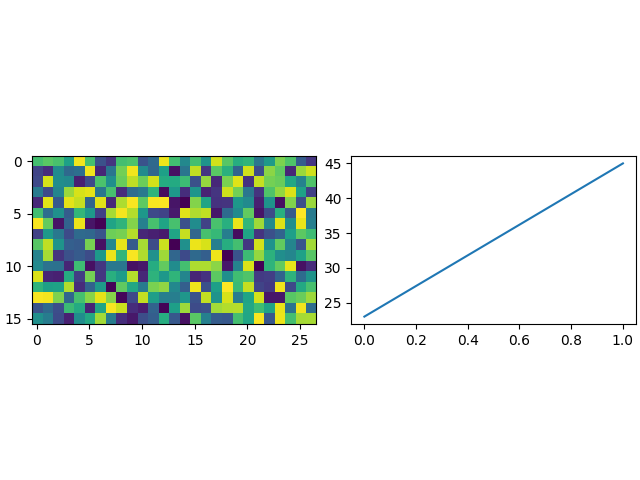
Beim Erstellen eines Bilddiagramms mit festem Datenverhältnis und dem Standardwert adjustable="box" neben einem normalen Diagramm wären die Achsen in der Höhe ungleich. set_box_aspect bietet hierfür eine einfache Lösung, indem es den Achsen des normalen Diagramms erlaubt, die Bilddimensionen als Kastenverhältnis zu verwenden.

Dieses Beispiel zeigt auch, dass das begrenzte Layout gut mit einem festen Kastenverhältnis zusammenspielt.

fig4, (ax, ax2) = plt.subplots(ncols=2, layout="constrained")

np.random.seed(19680801)  # Fixing random state for reproducibility
im = np.random.rand(16, 27)
ax.imshow(im)

ax2.plot([23, 45])
ax2.set_box_aspect(im.shape[0]/im.shape[1])

plt.show()

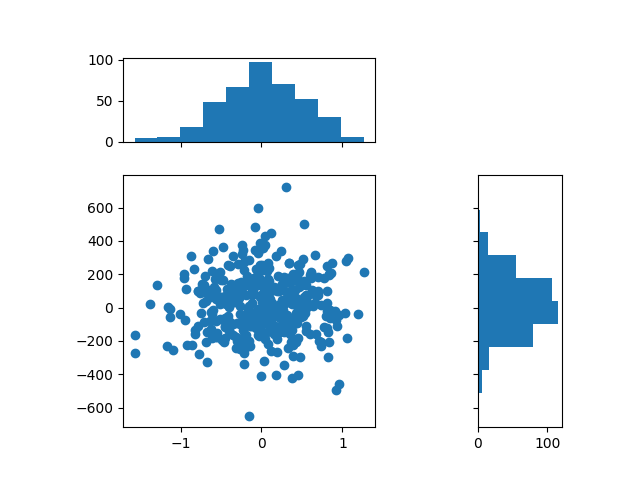
Quadratisches gemeinsames/marginales Diagramm

Es kann wünschenswert sein, marginale Verteilungen neben einem Diagramm gemeinsamer Daten anzuzeigen. Das Folgende erstellt ein quadratisches Diagramm, dessen marginale Achsen das Kastenverhältnis von Breiten- und Höhenverhältnissen des Gridspecs aufweisen. Dies stellt sicher, dass alle Achsen perfekt ausgerichtet sind, unabhängig von der Größe der Abbildung.

fig5, axs = plt.subplots(2, 2, sharex="col", sharey="row",
                         gridspec_kw=dict(height_ratios=[1, 3],
                                          width_ratios=[3, 1]))
axs[0, 1].set_visible(False)
axs[0, 0].set_box_aspect(1/3)
axs[1, 0].set_box_aspect(1)
axs[1, 1].set_box_aspect(3/1)

np.random.seed(19680801)  # Fixing random state for reproducibility
x, y = np.random.randn(2, 400) * [[.5], [180]]
axs[1, 0].scatter(x, y)
axs[0, 0].hist(x)
axs[1, 1].hist(y, orientation="horizontal")

plt.show()

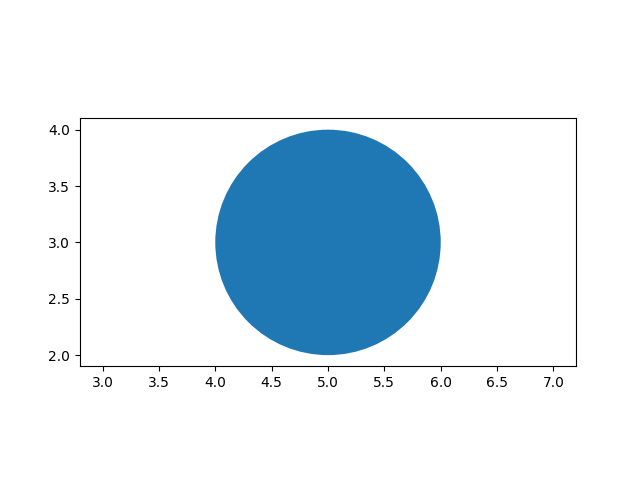
Datenverhältnis mit Kastenverhältnis einstellen

Beim Einstellen des Kastenverhältnisses kann auch das Datenverhältnis eingestellt werden. Hier erstellen wir eine Achse, die doppelt so lang wie hoch ist, und verwenden ein "gleiches" Datenverhältnis für ihren Inhalt, d. h. der Kreis bleibt tatsächlich kreisförmig.

fig6, ax = plt.subplots()

ax.add_patch(plt.Circle((5, 3), 1))
ax.set_aspect("equal", adjustable="datalim")
ax.set_box_aspect(0.5)
ax.autoscale()

plt.show()

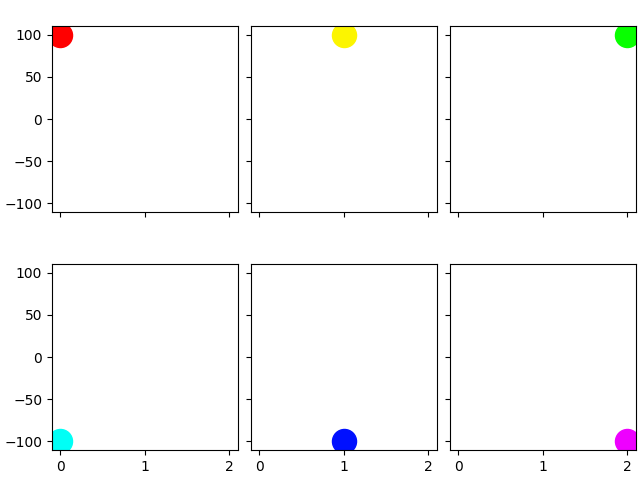
Kastenverhältnis für viele Unterdiagramme

Es ist möglich, das Kastenverhältnis bei der Initialisierung einer Achse zu übergeben. Das Folgende erstellt ein 2x3 Unterdiagramm-Raster mit lauter quadratischen Achsen.

fig7, axs = plt.subplots(2, 3, subplot_kw=dict(box_aspect=1),
                         sharex=True, sharey=True, layout="constrained")

for i, ax in enumerate(axs.flat):
    ax.scatter(i % 3, -((i // 3) - 0.5)*200, c=[plt.cm.hsv(i / 6)], s=300)
plt.show()

Referenzen

Die Verwendung der folgenden Funktionen, Methoden, Klassen und Module wird in diesem Beispiel gezeigt

• matplotlib.axes.Axes.set_box_aspect

Tags: Komponente: Achsen Styling: Größe Level: Anfänger