Transformations-Tutorial

Wie jedes Grafikpaket ist Matplotlib auf einem Transformationsrahmen aufgebaut, um einfach zwischen Koordinatensystemen zu wechseln: dem Daten-Koordinatensystem des Benutzers, dem Achsen-Koordinatensystem, dem Figuren-Koordinatensystem und dem Anzeige-Koordinatensystem. In 95 % Ihrer Diagramme müssen Sie nicht darüber nachdenken, da dies im Hintergrund geschieht. Wenn Sie jedoch die Grenzen der benutzerdefinierten Figurenerstellung ausreizen, ist es hilfreich, ein Verständnis für diese Objekte zu haben, damit Sie die von Matplotlib bereitgestellten Transformationen wiederverwenden oder eigene erstellen können (siehe matplotlib.transforms). Die folgende Tabelle fasst einige nützliche Koordinatensysteme, eine Beschreibung jedes Systems und das Transformations-Objekt für die Umwandlung von jedem Koordinatensystem in Anzeige-Koordinaten zusammen. In der Spalte "Transformations-Objekt" ist ax eine Axes-Instanz, fig ist eine Figure-Instanz und subfigure ist eine SubFigure-Instanz.

Koordinatensystem	Beschreibung	Transformations-Objekt vom System zur Anzeige
Daten	Das Koordinatensystem der Daten in den Achsen.	ax.transData
Achsen	Das Koordinatensystem der Achsen; (0, 0) ist unten links von den Achsen und (1, 1) ist oben rechts von den Achsen.	ax.transAxes
Subfigure	Das Koordinatensystem der SubFigure; (0, 0) ist unten links von der Subfigure und (1, 1) ist oben rechts von der Subfigure. Wenn eine Figur keine Subfiguren hat, ist dies dasselbe wie transFigure.	subfigure.transSubfigure
figure	Das Koordinatensystem der Figur; (0, 0) ist unten links von der Figur und (1, 1) ist oben rechts von der Figur.	fig.transFigure
Figur-Zoll	Das Koordinatensystem der Figur in Zoll; (0, 0) ist unten links von der Figur und (Breite, Höhe) ist oben rechts von der Figur in Zoll.	fig.dpi_scale_trans
x-Achse, y-Achse	Gemischte Koordinatensysteme, die Datenkoordinaten in einer Richtung und Achsenkoordinaten in der anderen verwenden.	ax.get_xaxis_transform(), ax.get_yaxis_transform()
Anzeige	Das native Koordinatensystem der Ausgabe; (0, 0) ist unten links vom Fenster und (Breite, Höhe) ist oben rechts von der Ausgabe in "Anzeigeeinheiten". Die genaue Interpretation der Einheiten hängt vom Backend ab. Zum Beispiel sind es Pixel für Agg und Punkte für svg/pdf.	None oder IdentityTransform()

Die Transform-Objekte sind sich des Quell- und Zielkoordinatensystems nicht bewusst. Die oben in der Tabelle genannten Objekte sind jedoch so konstruiert, dass sie Eingaben in ihrem Koordinatensystem entgegennehmen und in das Anzeige-Koordinatensystem umwandeln. Deshalb hat das Anzeige-Koordinatensystem None für die Spalte "Transformations-Objekt" – es ist bereits in Anzeige-Koordinaten. Die Benennungs- und Zielkonventionen sind eine Hilfe, um den Überblick über die verfügbaren "Standard"-Koordinatensysteme und Transformationen zu behalten.

Die Transformationen wissen auch, wie sie sich selbst invertieren können (über Transform.inverted), um eine Transformation vom Ausgabe-Koordinatensystem zurück zum Eingabe-Koordinatensystem zu erzeugen. Zum Beispiel konvertiert ax.transData Werte in Datenkoordinaten in Anzeige-Koordinaten und ax.transData.inverted() ist eine matplotlib.transforms.Transform, die von Anzeige-Koordinaten zu Datenkoordinaten geht. Dies ist besonders nützlich bei der Verarbeitung von Ereignissen aus der Benutzeroberfläche, die typischerweise im Anzeige-Raum auftreten und bei denen Sie wissen möchten, wo der Mausklick oder Tastendruck in Ihrem Daten-Koordinatensystem aufgetreten ist.

Beachten Sie, dass die Angabe der Position von Künstlern in Anzeige-Koordinaten ihre relative Position ändern kann, wenn sich die dpi oder die Größe der Figur ändern. Dies kann bei der Druckausgabe oder bei Änderungen der Bildschirmauflösung zu Verwirrung führen, da sich das Objekt in Position und Größe ändern kann. Daher ist es am gebräuchlichsten, dass Künstler, die in einer Achse oder Figur platziert werden, ihre Transformation auf etwas anderes als IdentityTransform() gesetzt haben; der Standardwert, wenn ein Künstler über add_artist zu einer Achse hinzugefügt wird, ist ax.transData, damit Sie in Daten-Koordinaten arbeiten und denken können und Matplotlib die Transformation in Anzeige übernimmt.

Datenkoordinaten

Beginnen wir mit der am häufigsten verwendeten Koordinate, dem Daten-Koordinatensystem. Jedes Mal, wenn Sie Daten zu den Achsen hinzufügen, aktualisiert Matplotlib die Datenlimits, die am häufigsten mit den Methoden set_xlim() und set_ylim() aktualisiert werden. Zum Beispiel reichen in der folgenden Figur die Datenlimits auf der x-Achse von 0 bis 10 und auf der y-Achse von -1 bis 1.

import matplotlib.pyplot as plt
import numpy as np

import matplotlib.patches as mpatches

x = np.arange(0, 10, 0.005)
y = np.exp(-x/2.) * np.sin(2*np.pi*x)

fig, ax = plt.subplots()
ax.plot(x, y)
ax.set_xlim(0, 10)
ax.set_ylim(-1, 1)

plt.show()

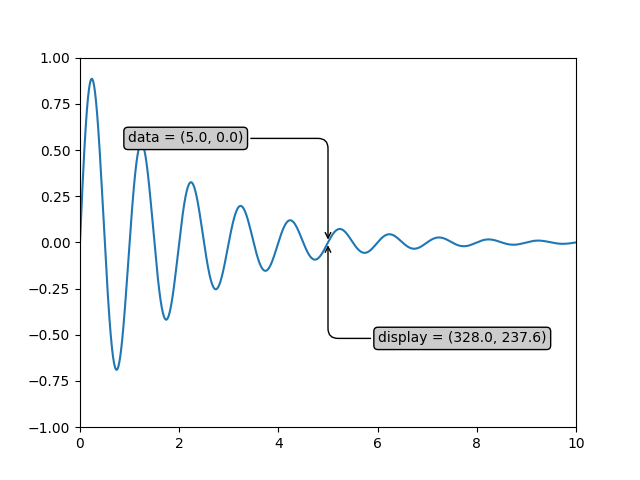
Sie können die ax.transData-Instanz verwenden, um von Ihren Daten in Ihr Anzeige-Koordinatensystem zu transformieren, entweder einen einzelnen Punkt oder eine Folge von Punkten, wie unten gezeigt.

In [14]: type(ax.transData)
Out[14]: <class 'matplotlib.transforms.CompositeGenericTransform'>

In [15]: ax.transData.transform((5, 0))
Out[15]: array([ 335.175,  247.   ])

In [16]: ax.transData.transform([(5, 0), (1, 2)])
Out[16]:
array([[ 335.175,  247.   ],
       [ 132.435,  642.2  ]])

Sie können die Methode inverted() verwenden, um eine Transformation zu erstellen, die Sie von Anzeige- zu Daten-Koordinaten führt.

In [41]: inv = ax.transData.inverted()

In [42]: type(inv)
Out[42]: <class 'matplotlib.transforms.CompositeGenericTransform'>

In [43]: inv.transform((335.175,  247.))
Out[43]: array([ 5.,  0.])

Wenn Sie diesen Tutorial-Text abtippen, können die genauen Werte der Anzeige-Koordinaten abweichen, wenn Sie eine andere Fenstergröße oder DPI-Einstellung haben. Ebenso sind in der folgenden Abbildung die als Anzeige beschrifteten Punkte wahrscheinlich nicht dieselben wie in der IPython-Sitzung, da die Standardeinstellungen für die Dokumentationsfigur anders sind.

x = np.arange(0, 10, 0.005)
y = np.exp(-x/2.) * np.sin(2*np.pi*x)

fig, ax = plt.subplots()
ax.plot(x, y)
ax.set_xlim(0, 10)
ax.set_ylim(-1, 1)

xdata, ydata = 5, 0
# This computing the transform now, if anything
# (figure size, dpi, axes placement, data limits, scales..)
# changes re-calling transform will get a different value.
xdisplay, ydisplay = ax.transData.transform((xdata, ydata))

bbox = dict(boxstyle="round", fc="0.8")
arrowprops = dict(
    arrowstyle="->",
    connectionstyle="angle,angleA=0,angleB=90,rad=10")

offset = 72
ax.annotate(f'data = ({xdata:.1f}, {ydata:.1f})',
            (xdata, ydata), xytext=(-2*offset, offset), textcoords='offset points',
            bbox=bbox, arrowprops=arrowprops)

disp = ax.annotate(f'display = ({xdisplay:.1f}, {ydisplay:.1f})',
                   (xdisplay, ydisplay), xytext=(0.5*offset, -offset),
                   xycoords='figure pixels',
                   textcoords='offset points',
                   bbox=bbox, arrowprops=arrowprops)

plt.show()

Warnung

Wenn Sie den Quellcode des obigen Beispiels in einem GUI-Backend ausführen, stellen Sie möglicherweise auch fest, dass die beiden Pfeile für die Daten- und Anzeige-Annotationen nicht auf denselben Punkt zeigen. Dies liegt daran, dass der Anzeige-Punkt vor dem Anzeigen der Figur berechnet wurde und das GUI-Backend die Figur beim Erstellen möglicherweise leicht vergrößert. Der Effekt ist ausgeprägter, wenn Sie die Figur selbst vergrößern. Dies ist ein guter Grund, warum Sie selten im Anzeige-Raum arbeiten möchten, aber Sie können sich mit dem 'on_draw' Event verbinden, um Figuren-Koordinaten bei Zeichenereignissen zu aktualisieren. Siehe Ereignisbehandlung und Auswahl.

Wenn Sie die x- oder y-Limits Ihrer Achsen ändern, werden die Datenlimits aktualisiert, sodass die Transformation einen neuen Anzeige-Punkt ergibt. Beachten Sie, dass nur die y-Anzeigekoordinate geändert wird, wenn wir nur die y-Limits ändern, und dass beide geändert werden, wenn wir auch die x-Limits ändern. Mehr dazu später, wenn wir über die Bbox sprechen.

In [54]: ax.transData.transform((5, 0))
Out[54]: array([ 335.175,  247.   ])

In [55]: ax.set_ylim(-1, 2)
Out[55]: (-1, 2)

In [56]: ax.transData.transform((5, 0))
Out[56]: array([ 335.175     ,  181.13333333])

In [57]: ax.set_xlim(10, 20)
Out[57]: (10, 20)

In [58]: ax.transData.transform((5, 0))
Out[58]: array([-171.675     ,  181.13333333])

Achsenkoordinaten

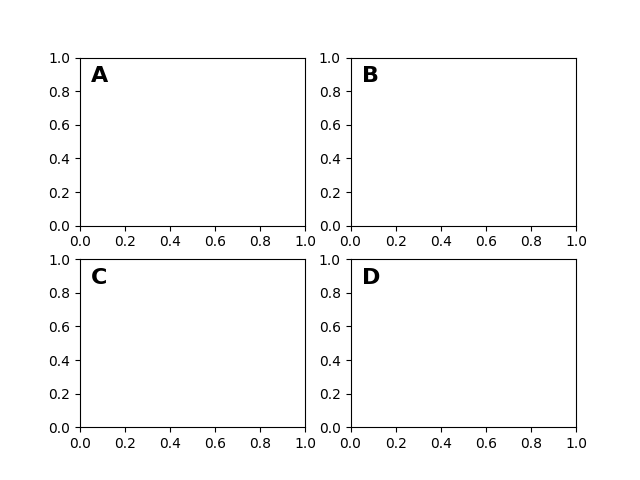
Nach dem Daten-Koordinatensystem ist Achsen wahrscheinlich das zweitnützlichste Koordinatensystem. Hier ist der Punkt (0, 0) die untere linke Ecke Ihrer Achsen oder Teilung, (0,5, 0,5) ist die Mitte und (1,0, 1,0) ist die obere rechte Ecke. Sie können auch auf Punkte außerhalb des Bereichs verweisen, sodass (-0,1, 1,1) links und oberhalb Ihrer Achsen liegt. Dieses Koordinatensystem ist äußerst nützlich beim Platzieren von Text in Ihren Achsen, da Sie oft eine Textblase an einer festen Position, z. B. oben links im Achsenbereich, haben möchten und diese Position beim Schwenken oder Zoomen beibehalten möchten. Hier ist ein einfaches Beispiel, das vier Panels erstellt und sie wie in Zeitschriften üblich mit 'A', 'B', 'C', 'D' beschriftet. Ein ausgefeilterer Ansatz für eine solche Beschriftung wird unter Beschriftung von Teilfiguren vorgestellt.

fig = plt.figure()
for i, label in enumerate(('A', 'B', 'C', 'D')):
    ax = fig.add_subplot(2, 2, i+1)
    ax.text(0.05, 0.95, label, transform=ax.transAxes,
            fontsize=16, fontweight='bold', va='top')

plt.show()

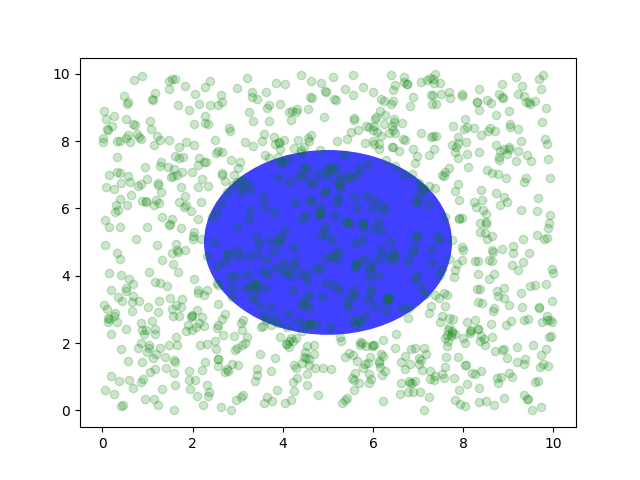
Sie können auch Linien oder Flächen im Achsen-Koordinatensystem zeichnen, aber das ist meiner Erfahrung nach weniger nützlich als die Verwendung von ax.transAxes zum Platzieren von Text. Dennoch ist hier ein albernes Beispiel, das einige zufällige Punkte im Datenraum zeichnet und einen halbtransparenten Kreis in der Mitte der Achsen mit einem Radius von einem Viertel der Achsen überlagert – wenn Ihre Achsen kein gleiches Seitenverhältnis beibehalten (siehe set_aspect()), sieht dies wie eine Ellipse aus. Verwenden Sie das Schwenk-/Zoom-Werkzeug, um sich zu bewegen, oder ändern Sie manuell die Daten-xlim und ylim, und Sie werden sehen, dass sich die Daten bewegen, aber der Kreis bleibt fixiert, da er sich nicht in Daten-Koordinaten befindet und immer in der Mitte der Achsen bleibt.

fig, ax = plt.subplots()
x, y = 10*np.random.rand(2, 1000)
ax.plot(x, y, 'go', alpha=0.2)  # plot some data in data coordinates

circ = mpatches.Circle((0.5, 0.5), 0.25, transform=ax.transAxes,
                       facecolor='blue', alpha=0.75)
ax.add_patch(circ)
plt.show()

Gemischte Transformationen

Das Zeichnen in gemischten Koordinatenräumen, die Achsen mit Daten-Koordinaten mischen, ist äußerst nützlich, um beispielsweise einen horizontalen Bereich zu erstellen, der einen bestimmten Bereich der y-Daten hervorhebt, aber sich über die x-Achse erstreckt, unabhängig von den Datenlimits, dem Schwenk- oder Zoomniveau usw. Tatsächlich sind diese gemischten Linien und Bereiche so nützlich, dass wir eingebaute Funktionen haben, um sie einfach zu zeichnen (siehe axhline(), axvline(), axhspan(), axvspan()), aber zu didaktischen Zwecken werden wir hier den horizontalen Bereich mit einer gemischten Transformation implementieren. Dieser Trick funktioniert nur für trennbare Transformationen, wie Sie sie in normalen kartesischen Koordinatensystemen sehen, aber nicht für untrennbare Transformationen wie die PolarTransform.

import matplotlib.transforms as transforms

fig, ax = plt.subplots()
x = np.random.randn(1000)

ax.hist(x, 30)
ax.set_title(r'$\sigma=1 \/ \dots \/ \sigma=2$', fontsize=16)

# the x coords of this transformation are data, and the y coord are axes
trans = transforms.blended_transform_factory(
    ax.transData, ax.transAxes)
# highlight the 1..2 stddev region with a span.
# We want x to be in data coordinates and y to span from 0..1 in axes coords.
rect = mpatches.Rectangle((1, 0), width=1, height=1, transform=trans,
                          color='yellow', alpha=0.5)
ax.add_patch(rect)

plt.show()

Hinweis

Die gemischten Transformationen, bei denen x in Daten-Koordinaten und y in Achsen-Koordinaten vorliegt, sind so nützlich, dass wir Hilfsmethoden haben, um die Versionen zurückzugeben, die Matplotlib intern zum Zeichnen von Ticks, Tick-Beschriftungen usw. verwendet. Die Methoden sind matplotlib.axes.Axes.get_xaxis_transform() und matplotlib.axes.Axes.get_yaxis_transform(). In dem obigen Beispiel kann der Aufruf von blended_transform_factory() durch get_xaxis_transform ersetzt werden.

trans = ax.get_xaxis_transform()

Zeichnen in physikalischen Koordinaten

Manchmal möchten wir, dass ein Objekt eine bestimmte physikalische Größe auf dem Diagramm hat. Hier zeichnen wir den gleichen Kreis wie oben, aber in physikalischen Koordinaten. Wenn dies interaktiv geschieht, können Sie sehen, dass die Änderung der Figurengröße den Abstand des Kreises von der unteren linken Ecke nicht ändert, seine Größe nicht ändert und der Kreis unabhängig vom Seitenverhältnis der Achsen ein Kreis bleibt.

fig, ax = plt.subplots(figsize=(5, 4))
x, y = 10*np.random.rand(2, 1000)
ax.plot(x, y*10., 'go', alpha=0.2)  # plot some data in data coordinates
# add a circle in fixed-coordinates
circ = mpatches.Circle((2.5, 2), 1.0, transform=fig.dpi_scale_trans,
                       facecolor='blue', alpha=0.75)
ax.add_patch(circ)
plt.show()

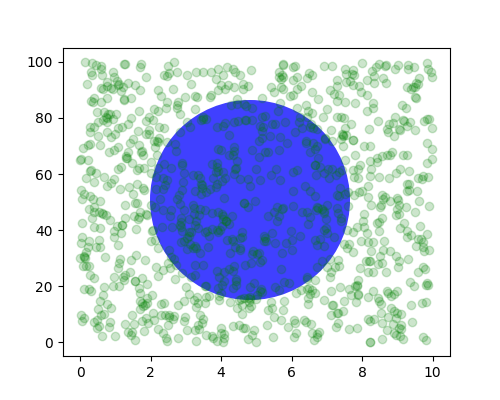
Wenn wir die Figurengröße ändern, ändert sich die absolute Position des Kreises nicht und er wird abgeschnitten.

fig, ax = plt.subplots(figsize=(7, 2))
x, y = 10*np.random.rand(2, 1000)
ax.plot(x, y*10., 'go', alpha=0.2)  # plot some data in data coordinates
# add a circle in fixed-coordinates
circ = mpatches.Circle((2.5, 2), 1.0, transform=fig.dpi_scale_trans,
                       facecolor='blue', alpha=0.75)
ax.add_patch(circ)
plt.show()

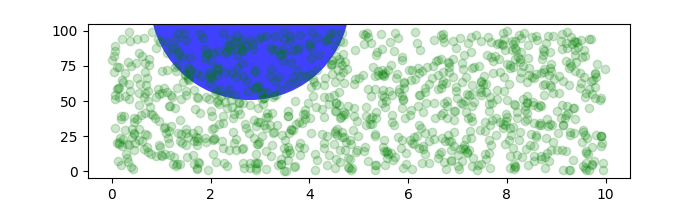
Ein weiterer Anwendungsfall ist das Platzieren einer Fläche mit einer festgelegten physikalischen Abmessung um einen Datenpunkt auf den Achsen. Hier addieren wir zwei Transformationen. Die erste legt die Skalierung fest, wie groß die Ellipse sein soll, und die zweite legt ihre Position fest. Die Ellipse wird dann am Ursprung platziert, und wir verwenden die Hilfstransformation ScaledTranslation, um sie an die richtige Stelle im ax.transData-Koordinatensystem zu verschieben. Diese Hilfsfunktion wird instanziiert mit

trans = ScaledTranslation(xt, yt, scale_trans)

wobei xt und yt die Verschiebungsabstände sind und scale_trans eine Transformation ist, die xt und yt zur Transformationszeit skaliert, bevor die Abstände angewendet werden.

Beachten Sie die Verwendung des Plusoperators für die Transformationen unten. Dieser Code besagt: Wenden Sie zuerst die Skalierungstransformation fig.dpi_scale_trans an, um die Ellipse auf die richtige Größe zu bringen, aber immer noch bei (0, 0) zentriert, und verschieben Sie dann die Daten zu xdata[0] und ydata[0] im Datenraum.

Bei interaktiver Nutzung bleibt die Ellipse gleich groß, auch wenn die Achsenlimits durch Zoomen geändert werden.

fig, ax = plt.subplots()
xdata, ydata = (0.2, 0.7), (0.5, 0.5)
ax.plot(xdata, ydata, "o")
ax.set_xlim((0, 1))

trans = (fig.dpi_scale_trans +
         transforms.ScaledTranslation(xdata[0], ydata[0], ax.transData))

# plot an ellipse around the point that is 150 x 130 points in diameter...
circle = mpatches.Ellipse((0, 0), 150/72, 130/72, angle=40,
                          fill=None, transform=trans)
ax.add_patch(circle)
plt.show()

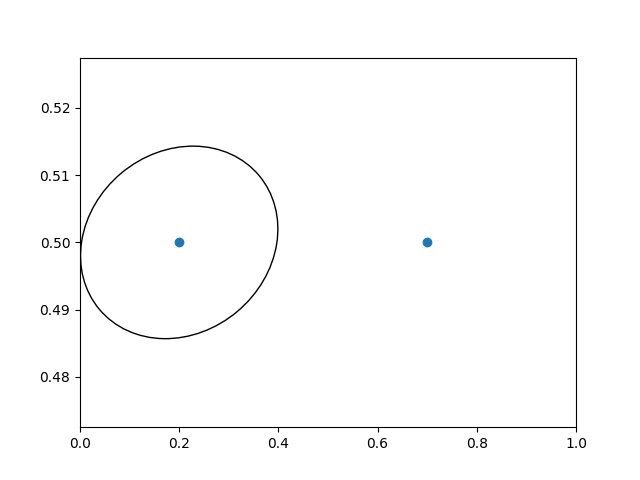
Hinweis

Die Reihenfolge der Transformation hat Auswirkungen. Hier erhält die Ellipse zuerst die richtigen Dimensionen im Anzeige-Raum und wird dann im Daten-Raum an die richtige Stelle verschoben. Hätten wir zuerst die ScaledTranslation angewendet, wären xdata[0] und ydata[0] zuerst in Anzeige-Koordinaten transformiert worden (auf einem 200-DPI-Monitor [358.4  475.2]) und dann wären diese Koordinaten von fig.dpi_scale_trans skaliert worden, wodurch das Zentrum der Ellipse weit außerhalb des Bildschirms gerückt wäre (d.h. [71680.  95040.]).

Verwendung von Offset-Transformationen zur Erzeugung eines Schatteneffekts

Ein weiterer Anwendungsfall für ScaledTranslation ist die Erstellung einer neuen Transformation, die von einer anderen Transformation versetzt ist, z. B. um ein Objekt relativ zu einem anderen Objekt leicht versetzt zu platzieren. Typischerweise möchten Sie, dass der Versatz in einer physikalischen Dimension, z. B. Punkten oder Zoll, und nicht in Daten-Koordinaten erfolgt, sodass der Versatzeffekt bei unterschiedlichen Zoomstufen und DPI-Einstellungen konstant bleibt.

Ein Anwendungsfall für einen Versatz ist die Erzeugung eines Schatteneffekts, bei dem Sie ein Objekt zeichnen, das identisch mit dem ersten ist, etwas nach rechts und etwas nach unten davon, und dabei die zorder anpassen, um sicherzustellen, dass der Schatten zuerst gezeichnet wird und dann das Objekt, das er überschattet, darüber.

Hier wenden wir die Transformationen in der entgegengesetzten Reihenfolge wie bei der Verwendung von ScaledTranslation oben an. Die Zeichnung wird zuerst in Datenkoordinaten (ax.transData) erstellt und dann um dx und dy Punkte mithilfe von fig.dpi_scale_trans verschoben. (In der Typografie ist ein Punkt 1/72 Zoll. Indem Sie Ihre Abstände in Punkten angeben, sieht Ihre Figur unabhängig von der gespeicherten DPI-Auflösung gleich aus.)

fig, ax = plt.subplots()

# make a simple sine wave
x = np.arange(0., 2., 0.01)
y = np.sin(2*np.pi*x)
line, = ax.plot(x, y, lw=3, color='blue')

# shift the object over 2 points, and down 2 points
dx, dy = 2/72., -2/72.
offset = transforms.ScaledTranslation(dx, dy, fig.dpi_scale_trans)
shadow_transform = ax.transData + offset

# now plot the same data with our offset transform;
# use the zorder to make sure we are below the line
ax.plot(x, y, lw=3, color='gray',
        transform=shadow_transform,
        zorder=0.5*line.get_zorder())

ax.set_title('creating a shadow effect with an offset transform')
plt.show()

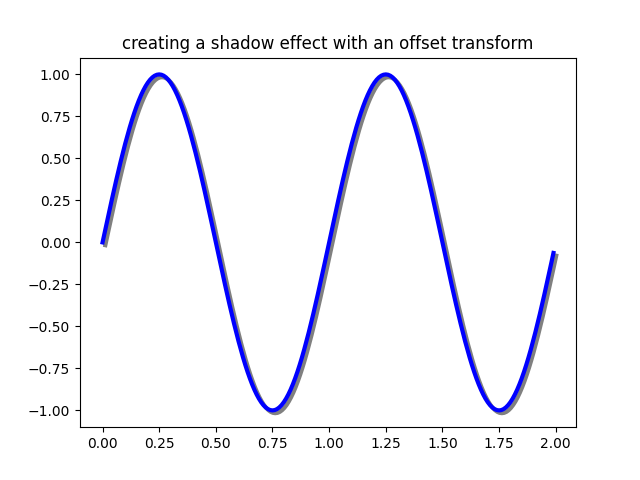
Hinweis

Der DPI- und Zoll-Abstand ist ein so häufiger Anwendungsfall, dass wir eine spezielle Hilfsfunktion haben, um ihn in matplotlib.transforms.offset_copy() zu erstellen, die eine neue Transformation mit einem hinzugefügten Abstand zurückgibt. Oben hätten wir also machen können:

shadow_transform = transforms.offset_copy(ax.transData,
         fig, dx, dy, units='inches')

Die Transformationspipeline

Die ax.transData-Transformation, mit der wir in diesem Tutorial gearbeitet haben, ist eine Zusammensetzung aus drei verschiedenen Transformationen, die die Transformationspipeline von Daten -> Anzeige-Koordinaten bilden. Michael Droettboom implementierte das Transformationsframework und sorgte für eine saubere API, die die nichtlinearen Projektionen und Skalierungen, die in polaren und logarithmischen Diagrammen auftreten, von den linearen affinen Transformationen trennt, die beim Schwenken und Zoomen auftreten. Hier liegt eine Effizienz vor, da Sie in Ihren Achsen schwenken und zoomen können, was die affine Transformation beeinflusst, aber Sie müssen die potenziell teuren nichtlinearen Skalierungen oder Projektionen bei einfachen Navigationsereignissen möglicherweise nicht berechnen. Es ist auch möglich, affine Transformationsmatrizen miteinander zu multiplizieren und sie dann in einem Schritt auf Koordinaten anzuwenden. Dies gilt nicht für alle möglichen Transformationen.

So wird die ax.transData-Instanz in der grundlegenden, trennbaren Achsenklasse Axes definiert.

self.transData = self.transScale + (self.transLimits + self.transAxes)

Wir haben die transAxes-Instanz bereits in Achsenkoordinaten kennengelernt, die die Ecken (0, 0) und (1, 1) des Achsen- oder Teilfiguren-Begrenzungsrahmens in den Anzeige-Raum abbildet. Betrachten wir also die beiden anderen Teile.

self.transLimits ist die Transformation, die Sie von Daten zu Achsen-Koordinaten führt; d. h., sie bildet Ihre sichtbaren xlim und ylim auf den Einheitsraum der Achsen ab (und transAxes wandelt diesen Einheitsraum dann in den Anzeige-Raum um). Wir können dies hier in Aktion sehen.

In [80]: ax = plt.subplot()

In [81]: ax.set_xlim(0, 10)
Out[81]: (0, 10)

In [82]: ax.set_ylim(-1, 1)
Out[82]: (-1, 1)

In [84]: ax.transLimits.transform((0, -1))
Out[84]: array([ 0.,  0.])

In [85]: ax.transLimits.transform((10, -1))
Out[85]: array([ 1.,  0.])

In [86]: ax.transLimits.transform((10, 1))
Out[86]: array([ 1.,  1.])

In [87]: ax.transLimits.transform((5, 0))
Out[87]: array([ 0.5,  0.5])

Und wir können diese gleiche invertierte Transformation verwenden, um von den Einheits-Achsen-Koordinaten zurück zu den Daten-Koordinaten zu gelangen.

In [90]: inv.transform((0.25, 0.25))
Out[90]: array([ 2.5, -0.5])

Der letzte Teil ist das Attribut self.transScale, das für die optionale nichtlineare Skalierung der Daten verantwortlich ist, z. B. für logarithmische Achsen. Wenn eine Achse initial eingerichtet wird, ist dies nur die Identitätstransformation, da die grundlegenden Matplotlib-Achsen eine lineare Skalierung haben. Wenn Sie jedoch eine logarithmische Skalierungsfunktion wie semilogx() aufrufen oder die Skalierung explizit mit set_xscale() auf logarithmisch setzen, wird das Attribut ax.transScale so gesetzt, dass es die nichtlineare Projektion behandelt. Die Skalierungstransformationen sind Eigenschaften der jeweiligen Axis-Instanzen xaxis und yaxis. Wenn Sie beispielsweise ax.set_xscale('log') aufrufen, aktualisiert die x-Achse ihre Skalierung auf eine matplotlib.scale.LogScale-Instanz.

Für nicht-trennbare Achsen wie PolarAxes gibt es ein weiteres Element zu berücksichtigen: die Projektionstransformation. Die transData der matplotlib.projections.polar.PolarAxes ist ähnlich wie bei den typischen trennbaren Matplotlib-Achsen, mit einem zusätzlichen Teil transProjection.

self.transData = (
    self.transScale + self.transShift + self.transProjection +
    (self.transProjectionAffine + self.transWedge + self.transAxes))

transProjection behandelt die Projektion vom Raum, z. B. Breitengrad und Längengrad für Kartendaten oder Radius und Theta für Polardaten, in ein trennbares kartesisches Koordinatensystem. Es gibt mehrere Projektionsbeispiele im Paket matplotlib.projections, und der beste Weg, mehr zu erfahren, ist, den Quellcode dieser Pakete zu öffnen und zu sehen, wie Sie Ihre eigenen erstellen können, da Matplotlib erweiterbare Achsen und Projektionen unterstützt. Michael Droettboom hat ein schönes Tutorial-Beispiel zur Erstellung von Hammer-Projektionsachsen bereitgestellt. Siehe Benutzerdefinierte Projektion.