Colormap-Normalisierung

Objekte, die standardmäßig Colormaps verwenden, bilden die Farben in der Colormap linear von den Datenwerten vmin bis vmax ab. Zum Beispiel

pcm = ax.pcolormesh(x, y, Z, vmin=-1., vmax=1., cmap='RdBu_r')

bildet die Daten in Z linear von -1 bis +1 ab, sodass Z=0 eine Farbe in der Mitte der Colormap RdBu_r (in diesem Fall Weiß) ergibt.

Matplotlib führt diese Abbildung in zwei Schritten durch: Zuerst erfolgt eine Normalisierung von den Eingabedaten auf [0, 1], und dann wird auf die Indizes in der Colormap abgebildet. Normalisierungen sind Klassen, die im Modul matplotlib.colors() definiert sind. Die Standard-Normalisierung ist die lineare Normalisierung matplotlib.colors.Normalize().

Künstler, die Daten auf Farbe abbilden, übergeben die Argumente vmin und vmax, um eine matplotlib.colors.Normalize() Instanz zu erstellen, und rufen diese dann auf

>>> import matplotlib as mpl
>>> norm = mpl.colors.Normalize(vmin=-1, vmax=1)
>>> norm(0)
0.5

Es gibt jedoch Fälle, in denen es nützlich ist, Daten nichtlinear auf Colormaps abzubilden.

Logarithmisch

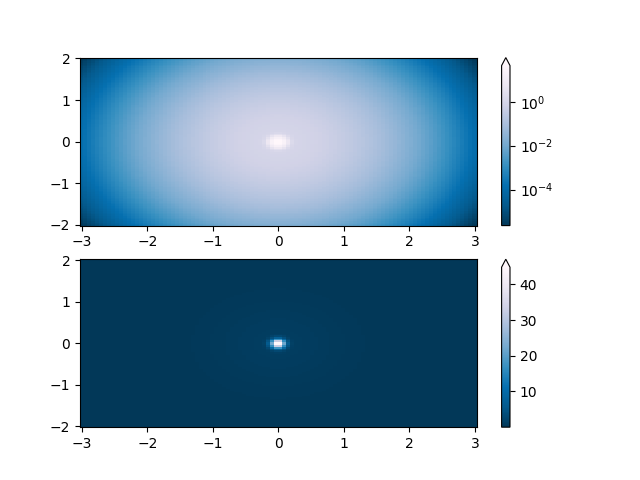
Eine der gebräuchlichsten Transformationen ist die Darstellung von Daten durch ihren Logarithmus (zur Basis 10). Diese Transformation ist nützlich, um Änderungen über sehr unterschiedliche Skalen hinweg darzustellen. Mit colors.LogNorm werden die Daten mittels \(log_{10}\) normalisiert. Im folgenden Beispiel gibt es zwei Buckel, einen viel kleiner als den anderen. Mit colors.LogNorm können die Form und Lage jedes Buckels deutlich gesehen werden

import matplotlib.pyplot as plt
import numpy as np

from matplotlib import cm
import matplotlib.cbook as cbook
import matplotlib.colors as colors

N = 100
X, Y = np.mgrid[-3:3:complex(0, N), -2:2:complex(0, N)]

# A low hump with a spike coming out of the top right.  Needs to have
# z/colour axis on a log scale, so we see both hump and spike. A linear
# scale only shows the spike.
Z1 = np.exp(-X**2 - Y**2)
Z2 = np.exp(-(X * 10)**2 - (Y * 10)**2)
Z = Z1 + 50 * Z2

fig, ax = plt.subplots(2, 1)

pcm = ax[0].pcolor(X, Y, Z,
                   norm=colors.LogNorm(vmin=Z.min(), vmax=Z.max()),
                   cmap='PuBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[0], extend='max')

pcm = ax[1].pcolor(X, Y, Z, cmap='PuBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[1], extend='max')
plt.show()

Zentriert

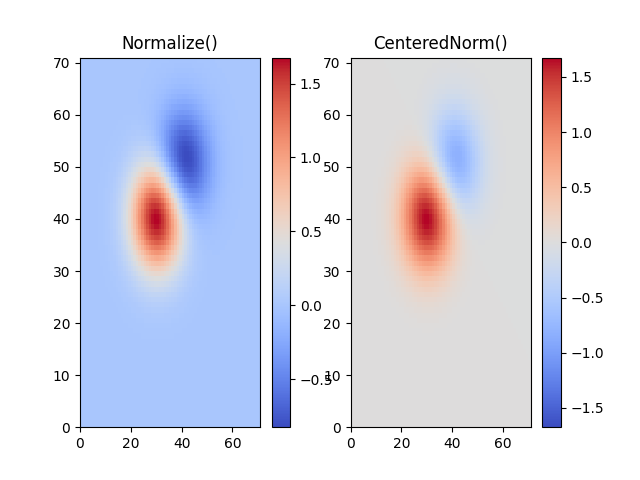
In vielen Fällen sind die Daten symmetrisch um ein Zentrum, zum Beispiel positive und negative Anomalien um ein Zentrum 0. In diesem Fall möchten wir, dass das Zentrum auf 0,5 abgebildet wird und der Datenpunkt mit der größten Abweichung vom Zentrum auf 1,0 abgebildet wird, wenn sein Wert größer als das Zentrum ist, oder andernfalls auf 0,0. Die Norm colors.CenteredNorm erstellt automatisch eine solche Abbildung. Sie eignet sich gut zur Kombination mit einer divergenten Colormap, die an den Rändern unterschiedliche Farben verwendet, die sich in der Mitte zu einer ungesättigten Farbe treffen.

Wenn das Symmetriezentrum von 0 abweicht, kann es mit dem Argument vcenter eingestellt werden. Für logarithmische Skalierung auf beiden Seiten des Zentrums siehe colors.SymLogNorm unten; um eine andere Abbildung oberhalb und unterhalb des Zentrums anzuwenden, verwenden Sie colors.TwoSlopeNorm unten.

delta = 0.1
x = np.arange(-3.0, 4.001, delta)
y = np.arange(-4.0, 3.001, delta)
X, Y = np.meshgrid(x, y)
Z1 = np.exp(-X**2 - Y**2)
Z2 = np.exp(-(X - 1)**2 - (Y - 1)**2)
Z = (0.9*Z1 - 0.5*Z2) * 2

# select a divergent colormap
cmap = cm.coolwarm

fig, (ax1, ax2) = plt.subplots(ncols=2)
pc = ax1.pcolormesh(Z, cmap=cmap)
fig.colorbar(pc, ax=ax1)
ax1.set_title('Normalize()')

pc = ax2.pcolormesh(Z, norm=colors.CenteredNorm(), cmap=cmap)
fig.colorbar(pc, ax=ax2)
ax2.set_title('CenteredNorm()')

plt.show()

Symmetrisch logarithmisch

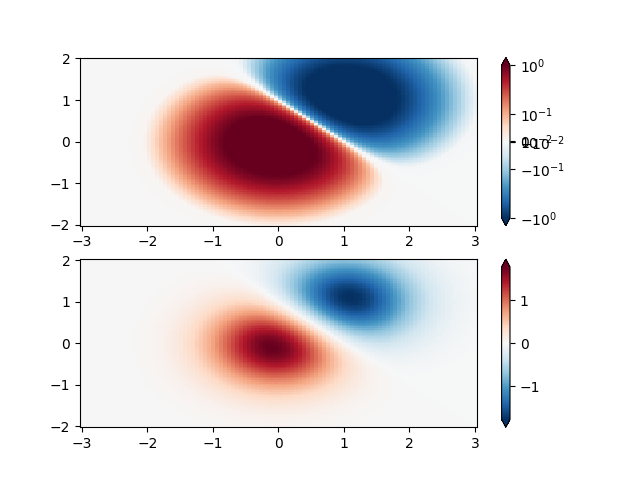
Ebenso kommt es manchmal vor, dass Daten sowohl positiv als auch negativ sind, wir aber dennoch eine logarithmische Skalierung auf beide anwenden möchten. In diesem Fall werden die negativen Zahlen ebenfalls logarithmisch skaliert und auf kleinere Zahlen abgebildet; z. B. wenn vmin=-vmax, dann werden die negativen Zahlen von 0 bis 0,5 und die positiven von 0,5 bis 1 abgebildet.

Da der Logarithmus von Werten nahe Null gegen Unendlich geht, muss ein kleiner Bereich um Null linear abgebildet werden. Der Parameter linthresh ermöglicht es dem Benutzer, die Größe dieses Bereichs (-linthresh, linthresh) anzugeben. Die Größe dieses Bereichs in der Colormap wird durch linscale bestimmt. Wenn linscale == 1.0 (Standard), entspricht der für die positiven und negativen Hälften des linearen Bereichs verwendete Raum dem einer Dekade im logarithmischen Bereich.

N = 100
X, Y = np.mgrid[-3:3:complex(0, N), -2:2:complex(0, N)]
Z1 = np.exp(-X**2 - Y**2)
Z2 = np.exp(-(X - 1)**2 - (Y - 1)**2)
Z = (Z1 - Z2) * 2

fig, ax = plt.subplots(2, 1)

pcm = ax[0].pcolormesh(X, Y, Z,
                       norm=colors.SymLogNorm(linthresh=0.03, linscale=0.03,
                                              vmin=-1.0, vmax=1.0, base=10),
                       cmap='RdBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[0], extend='both')

pcm = ax[1].pcolormesh(X, Y, Z, cmap='RdBu_r', vmin=-np.max(Z), shading='auto')
fig.colorbar(pcm, ax=ax[1], extend='both')
plt.show()

Potenzgesetz

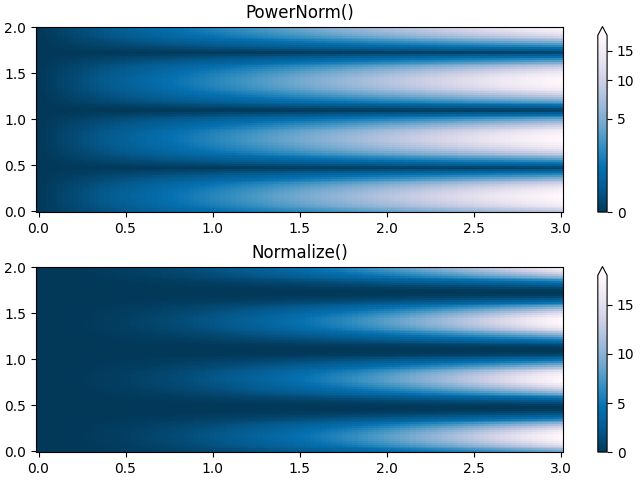
Manchmal ist es nützlich, die Farben auf eine Potenzgesetz-Beziehung abzubilden (d. h. \(y=x^{\gamma}\), wobei \(\gamma\) die Potenz ist). Hierfür verwenden wir colors.PowerNorm. Dieses nimmt gamma als Argument entgegen (gamma == 1.0 ergibt die Standard-Linear-Normalisierung)

Hinweis

Es sollte wahrscheinlich einen guten Grund geben, die Daten mit dieser Art von Transformation darzustellen. Technische Betrachter sind an lineare und logarithmische Achsen und Datentransformationen gewöhnt. Potenzgesetze sind weniger verbreitet, und Betrachter sollten explizit darauf hingewiesen werden, dass sie verwendet wurden.

N = 100
X, Y = np.mgrid[0:3:complex(0, N), 0:2:complex(0, N)]
Z1 = (1 + np.sin(Y * 10.)) * X**2

fig, ax = plt.subplots(2, 1, layout='constrained')

pcm = ax[0].pcolormesh(X, Y, Z1, norm=colors.PowerNorm(gamma=0.5),
                       cmap='PuBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[0], extend='max')
ax[0].set_title('PowerNorm()')

pcm = ax[1].pcolormesh(X, Y, Z1, cmap='PuBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[1], extend='max')
ax[1].set_title('Normalize()')
plt.show()

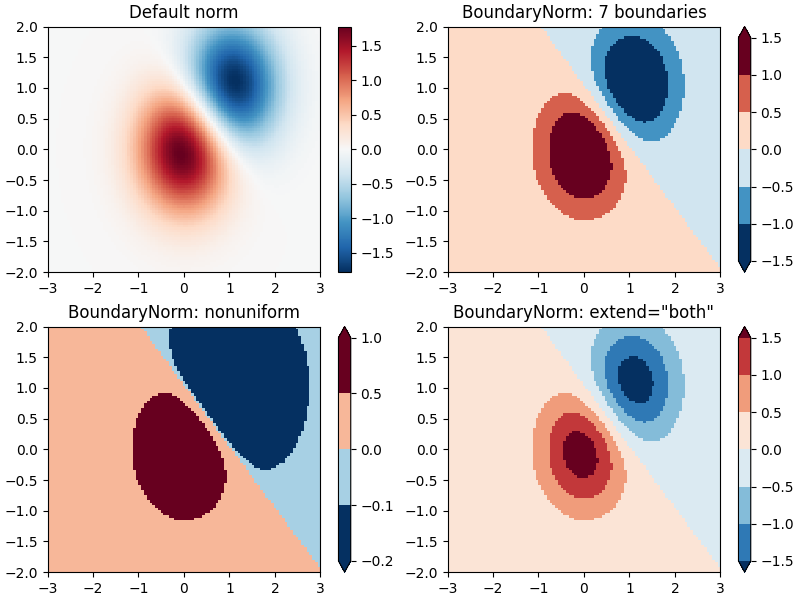
Diskrete Grenzen

Eine weitere von Matplotlib bereitgestellte Normalisierung ist colors.BoundaryNorm. Zusätzlich zu vmin und vmax nimmt sie als Argumente Grenzen entgegen, zwischen denen Daten abgebildet werden sollen. Die Farben werden dann linear zwischen diesen "Grenzen" verteilt. Sie kann auch ein extend Argument annehmen, um obere und/oder untere Werte außerhalb des Bereichs hinzuzufügen, über den die Farben verteilt werden. Zum Beispiel

>>> import matplotlib.colors as colors
>>> bounds = np.array([-0.25, -0.125, 0, 0.5, 1])
>>> norm = colors.BoundaryNorm(boundaries=bounds, ncolors=4)
>>> print(norm([-0.2, -0.15, -0.02, 0.3, 0.8, 0.99]))
[0 0 1 2 3 3]

Hinweis: Im Gegensatz zu den anderen Normen gibt diese Norm Werte von 0 bis ncolors-1 zurück.

N = 100
X, Y = np.meshgrid(np.linspace(-3, 3, N), np.linspace(-2, 2, N))
Z1 = np.exp(-X**2 - Y**2)
Z2 = np.exp(-(X - 1)**2 - (Y - 1)**2)
Z = ((Z1 - Z2) * 2)[:-1, :-1]

fig, ax = plt.subplots(2, 2, figsize=(8, 6), layout='constrained')
ax = ax.flatten()

# Default norm:
pcm = ax[0].pcolormesh(X, Y, Z, cmap='RdBu_r')
fig.colorbar(pcm, ax=ax[0], orientation='vertical')
ax[0].set_title('Default norm')

# Even bounds give a contour-like effect:
bounds = np.linspace(-1.5, 1.5, 7)
norm = colors.BoundaryNorm(boundaries=bounds, ncolors=256)
pcm = ax[1].pcolormesh(X, Y, Z, norm=norm, cmap='RdBu_r')
fig.colorbar(pcm, ax=ax[1], extend='both', orientation='vertical')
ax[1].set_title('BoundaryNorm: 7 boundaries')

# Bounds may be unevenly spaced:
bounds = np.array([-0.2, -0.1, 0, 0.5, 1])
norm = colors.BoundaryNorm(boundaries=bounds, ncolors=256)
pcm = ax[2].pcolormesh(X, Y, Z, norm=norm, cmap='RdBu_r')
fig.colorbar(pcm, ax=ax[2], extend='both', orientation='vertical')
ax[2].set_title('BoundaryNorm: nonuniform')

# With out-of-bounds colors:
bounds = np.linspace(-1.5, 1.5, 7)
norm = colors.BoundaryNorm(boundaries=bounds, ncolors=256, extend='both')
pcm = ax[3].pcolormesh(X, Y, Z, norm=norm, cmap='RdBu_r')
# The colorbar inherits the "extend" argument from BoundaryNorm.
fig.colorbar(pcm, ax=ax[3], orientation='vertical')
ax[3].set_title('BoundaryNorm: extend="both"')
plt.show()

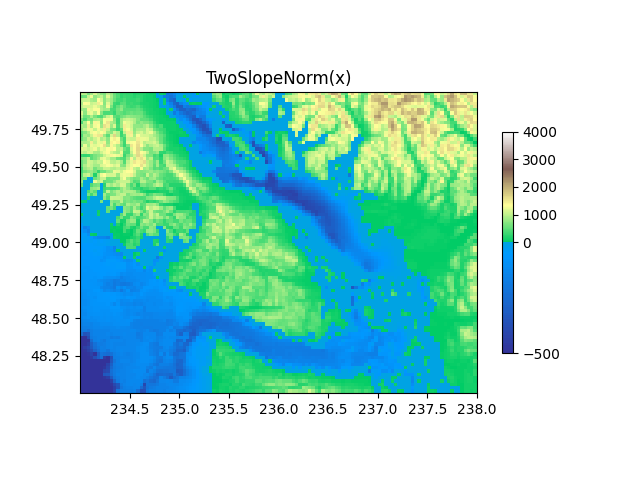
TwoSlopeNorm: Unterschiedliche Abbildung auf beiden Seiten eines Zentrums

Manchmal möchten wir eine andere Colormap auf beiden Seiten eines konzeptionellen Mittelpunkts haben, und wir möchten, dass diese beiden Colormaps unterschiedliche lineare Skalen haben. Ein Beispiel ist eine topografische Karte, bei der Land und Meer einen Mittelpunkt bei Null haben, aber das Land typischerweise einen größeren Höhenbereich als die Tiefe des Wassers hat und oft durch eine andere Colormap dargestellt wird.

dem = cbook.get_sample_data('topobathy.npz')
topo = dem['topo']
longitude = dem['longitude']
latitude = dem['latitude']

fig, ax = plt.subplots()
# make a colormap that has land and ocean clearly delineated and of the
# same length (256 + 256)
colors_undersea = plt.cm.terrain(np.linspace(0, 0.17, 256))
colors_land = plt.cm.terrain(np.linspace(0.25, 1, 256))
all_colors = np.vstack((colors_undersea, colors_land))
terrain_map = colors.LinearSegmentedColormap.from_list(
    'terrain_map', all_colors)

# make the norm:  Note the center is offset so that the land has more
# dynamic range:
divnorm = colors.TwoSlopeNorm(vmin=-500., vcenter=0, vmax=4000)

pcm = ax.pcolormesh(longitude, latitude, topo, rasterized=True, norm=divnorm,
                    cmap=terrain_map, shading='auto')
# Simple geographic plot, set aspect ratio because distance between lines of
# longitude depends on latitude.
ax.set_aspect(1 / np.cos(np.deg2rad(49)))
ax.set_title('TwoSlopeNorm(x)')
cb = fig.colorbar(pcm, shrink=0.6)
cb.set_ticks([-500, 0, 1000, 2000, 3000, 4000])
plt.show()

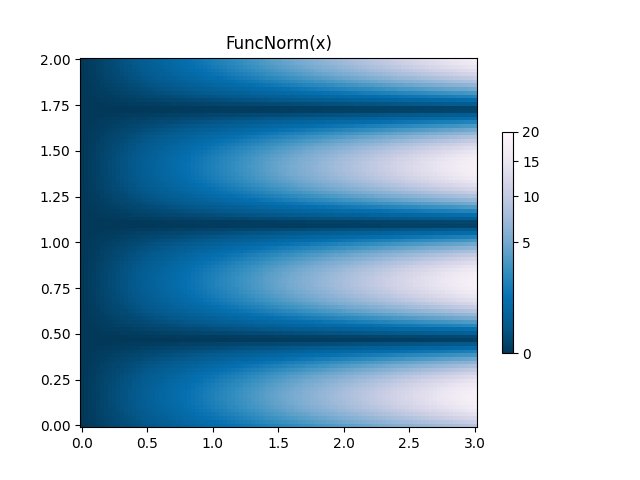
FuncNorm: Beliebige Funktionsnormalisierung

Wenn die oben genannten Normen nicht die gewünschte Normalisierung bieten, können Sie FuncNorm verwenden, um Ihre eigene zu definieren. Beachten Sie, dass dieses Beispiel dasselbe ist wie PowerNorm mit einer Potenz von 0,5

def _forward(x):
    return np.sqrt(x)


def _inverse(x):
    return x**2

N = 100
X, Y = np.mgrid[0:3:complex(0, N), 0:2:complex(0, N)]
Z1 = (1 + np.sin(Y * 10.)) * X**2
fig, ax = plt.subplots()

norm = colors.FuncNorm((_forward, _inverse), vmin=0, vmax=20)
pcm = ax.pcolormesh(X, Y, Z1, norm=norm, cmap='PuBu_r', shading='auto')
ax.set_title('FuncNorm(x)')
fig.colorbar(pcm, shrink=0.6)
plt.show()

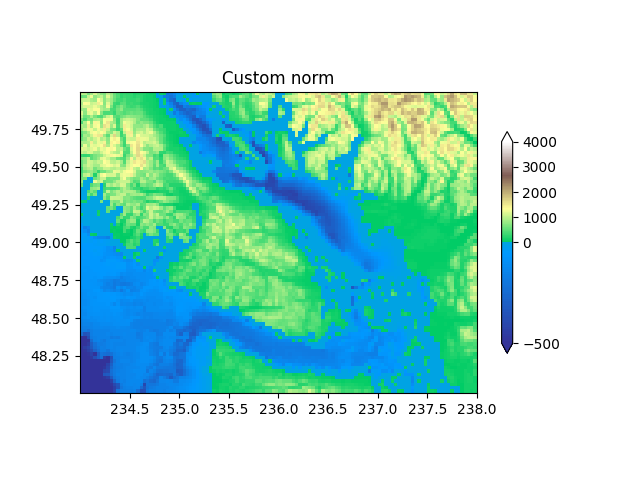
Benutzerdefinierte Normalisierung: Zwei lineare Bereiche manuell implementieren

Die oben beschriebene TwoSlopeNorm ist ein nützliches Beispiel für die Definition Ihrer eigenen Norm. Beachten Sie, dass Sie für das Funktionieren der Farbleiste eine Umkehrfunktion für Ihre Norm definieren müssen

class MidpointNormalize(colors.Normalize):
    def __init__(self, vmin=None, vmax=None, vcenter=None, clip=False):
        self.vcenter = vcenter
        super().__init__(vmin, vmax, clip)

    def __call__(self, value, clip=None):
        # I'm ignoring masked values and all kinds of edge cases to make a
        # simple example...
        # Note also that we must extrapolate beyond vmin/vmax
        x, y = [self.vmin, self.vcenter, self.vmax], [0, 0.5, 1.]
        return np.ma.masked_array(np.interp(value, x, y,
                                            left=-np.inf, right=np.inf))

    def inverse(self, value):
        y, x = [self.vmin, self.vcenter, self.vmax], [0, 0.5, 1]
        return np.interp(value, x, y, left=-np.inf, right=np.inf)


fig, ax = plt.subplots()
midnorm = MidpointNormalize(vmin=-500., vcenter=0, vmax=4000)

pcm = ax.pcolormesh(longitude, latitude, topo, rasterized=True, norm=midnorm,
                    cmap=terrain_map, shading='auto')
ax.set_aspect(1 / np.cos(np.deg2rad(49)))
ax.set_title('Custom norm')
cb = fig.colorbar(pcm, shrink=0.6, extend='both')
cb.set_ticks([-500, 0, 1000, 2000, 3000, 4000])

plt.show()