Achsenskalen

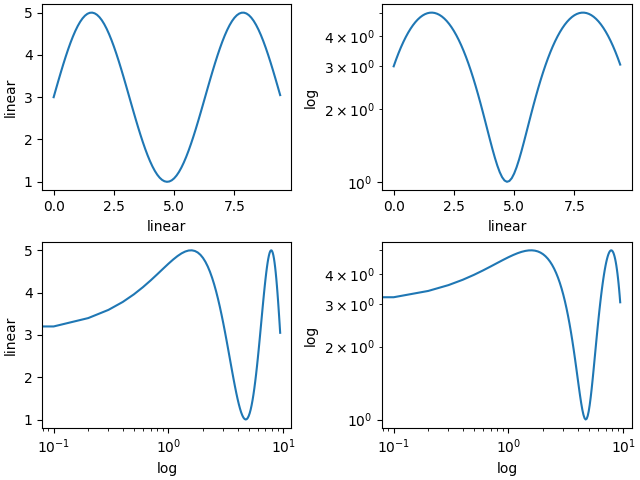
Standardmäßig zeigt Matplotlib Daten auf der Achse mit einer linearen Skala an. Matplotlib unterstützt auch logarithmische Skalen und andere, weniger gebräuchliche Skalen. Dies kann in der Regel direkt durch die Verwendung der Methoden set_xscale oder set_yscale erfolgen.

import matplotlib.pyplot as plt
import numpy as np

import matplotlib.scale as mscale
from matplotlib.ticker import FixedLocator, NullFormatter

fig, axs = plt.subplot_mosaic([['linear', 'linear-log'],
                               ['log-linear', 'log-log']], layout='constrained')

x = np.arange(0, 3*np.pi, 0.1)
y = 2 * np.sin(x) + 3

ax = axs['linear']
ax.plot(x, y)
ax.set_xlabel('linear')
ax.set_ylabel('linear')

ax = axs['linear-log']
ax.plot(x, y)
ax.set_yscale('log')
ax.set_xlabel('linear')
ax.set_ylabel('log')

ax = axs['log-linear']
ax.plot(x, y)
ax.set_xscale('log')
ax.set_xlabel('log')
ax.set_ylabel('linear')

ax = axs['log-log']
ax.plot(x, y)
ax.set_xscale('log')
ax.set_yscale('log')
ax.set_xlabel('log')
ax.set_ylabel('log')

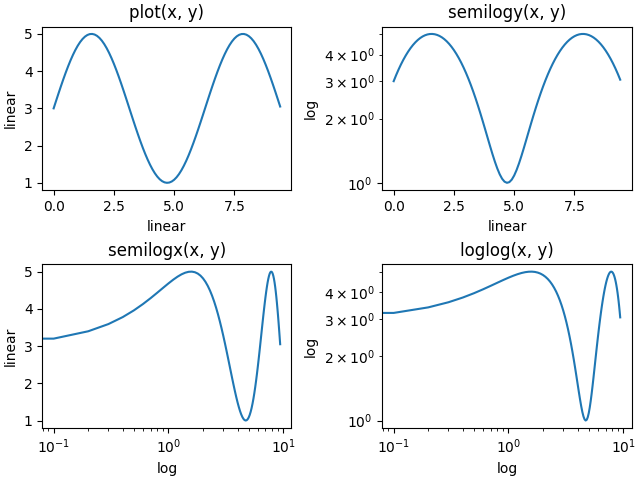
loglog und semilogx/y

Die logarithmische Achse wird so oft verwendet, dass es einige Hilfsfunktionen gibt, die dasselbe tun: semilogy, semilogx und loglog.

fig, axs = plt.subplot_mosaic([['linear', 'linear-log'],
                               ['log-linear', 'log-log']], layout='constrained')

x = np.arange(0, 3*np.pi, 0.1)
y = 2 * np.sin(x) + 3

ax = axs['linear']
ax.plot(x, y)
ax.set_xlabel('linear')
ax.set_ylabel('linear')
ax.set_title('plot(x, y)')

ax = axs['linear-log']
ax.semilogy(x, y)
ax.set_xlabel('linear')
ax.set_ylabel('log')
ax.set_title('semilogy(x, y)')

ax = axs['log-linear']
ax.semilogx(x, y)
ax.set_xlabel('log')
ax.set_ylabel('linear')
ax.set_title('semilogx(x, y)')

ax = axs['log-log']
ax.loglog(x, y)
ax.set_xlabel('log')
ax.set_ylabel('log')
ax.set_title('loglog(x, y)')

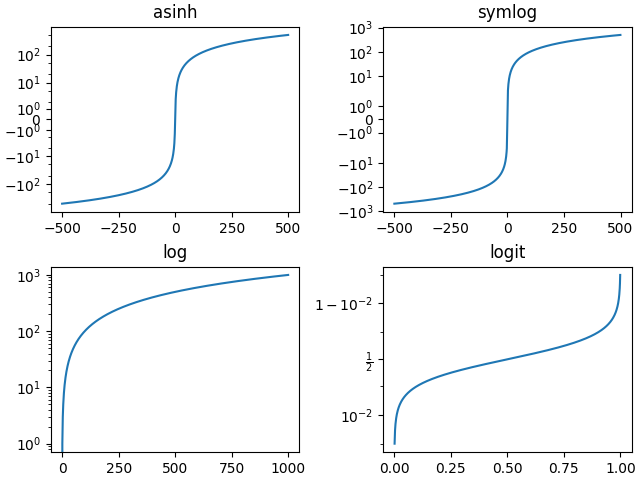
Andere integrierte Skalen

Es gibt andere Skalen, die verwendet werden können. Die Liste der registrierten Skalen kann von scale.get_scale_names abgerufen werden.

print(mscale.get_scale_names())

['asinh', 'function', 'functionlog', 'linear', 'log', 'logit', 'symlog']

fig, axs = plt.subplot_mosaic([['asinh', 'symlog'],
                               ['log', 'logit']], layout='constrained')

x = np.arange(0, 1000)

for name, ax in axs.items():
    if name in ['asinh', 'symlog']:
        yy = x - np.mean(x)
    elif name in ['logit']:
        yy = (x-np.min(x))
        yy = yy / np.max(np.abs(yy))
    else:
        yy = x

    ax.plot(yy, yy)
    ax.set_yscale(name)
    ax.set_title(name)

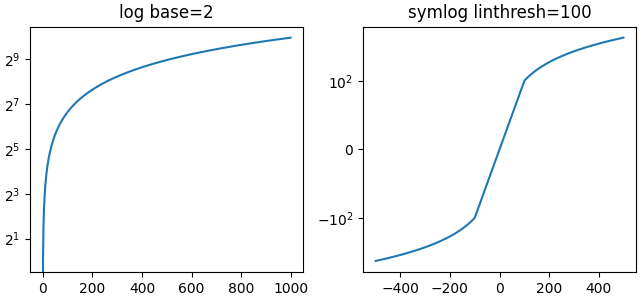
Optionale Argumente für Skalen

Einige der Standardskalen haben optionale Argumente. Diese sind in der API-Referenz für die entsprechenden Skalen unter scale dokumentiert. Man kann die Basis des zu plottenden Logarithmus (z. B. 2 unten) oder den linearen Schwellenwertbereich für 'symlog' ändern.

fig, axs = plt.subplot_mosaic([['log', 'symlog']], layout='constrained',
                              figsize=(6.4, 3))

for name, ax in axs.items():
    if name in ['log']:
        ax.plot(x, x)
        ax.set_yscale('log', base=2)
        ax.set_title('log base=2')
    else:
        ax.plot(x - np.mean(x), x - np.mean(x))
        ax.set_yscale('symlog', linthresh=100)
        ax.set_title('symlog linthresh=100')

Arbiträre Funktionsskalen

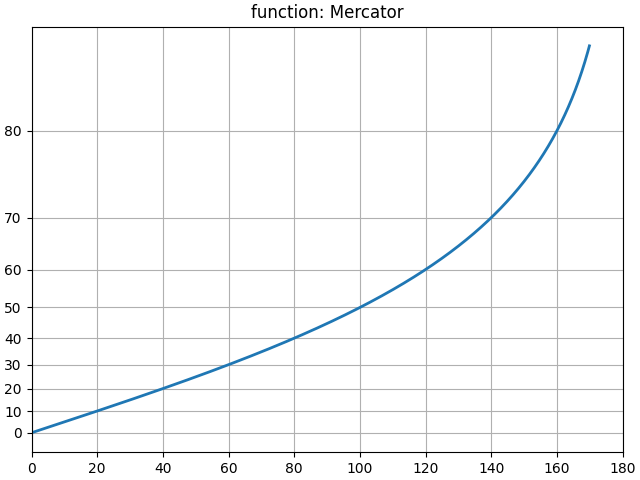
Benutzer können eine vollständige Skalenklasse definieren und diese an set_xscale und set_yscale übergeben (siehe Benutzerdefinierte Skala). Eine Abkürzung dafür ist die Verwendung der Skala 'function' und die Übergabe einer forward- und einer inverse-Funktion als zusätzliche Argumente. Das Folgende führt eine Mercator-Transformation für die y-Achse durch.

# Function Mercator transform
def forward(a):
    a = np.deg2rad(a)
    return np.rad2deg(np.log(np.abs(np.tan(a) + 1.0 / np.cos(a))))


def inverse(a):
    a = np.deg2rad(a)
    return np.rad2deg(np.arctan(np.sinh(a)))


t = np.arange(0, 170.0, 0.1)
s = t / 2.

fig, ax = plt.subplots(layout='constrained')
ax.plot(t, s, '-', lw=2)

ax.set_yscale('function', functions=(forward, inverse))
ax.set_title('function: Mercator')
ax.grid(True)
ax.set_xlim([0, 180])
ax.yaxis.set_minor_formatter(NullFormatter())
ax.yaxis.set_major_locator(FixedLocator(np.arange(0, 90, 10)))

Was ist eine "Skala"?

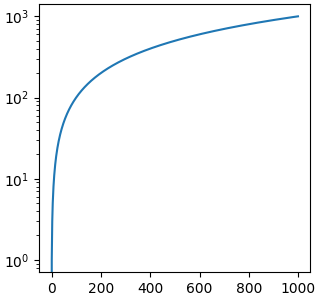
Eine Skala ist ein Objekt, das an einer Achse angebracht wird. Die Klassendokumentation befindet sich unter scale. set_xscale und set_yscale legen die Skala auf den jeweiligen Achsenobjekten fest. Sie können die Skala auf einer Achse mit get_scale ermitteln.

fig, ax = plt.subplots(layout='constrained',
                              figsize=(3.2, 3))
ax.semilogy(x, x)

print(ax.xaxis.get_scale())
print(ax.yaxis.get_scale())

linear
log

Das Festlegen einer Skala bewirkt drei Dinge. Erstens definiert sie eine Transformation auf der Achse, die zwischen Datenwerten und Positionen entlang der Achse abbildet. Diese Transformation kann über get_transform abgerufen werden.

print(ax.yaxis.get_transform())

LogTransform(base=10, nonpositive='clip')

Transformationen auf der Achse sind ein relativ niedrigstufiges Konzept, aber sie sind eine der wichtigen Rollen, die set_scale spielt.

Das Festlegen der Skala setzt auch Standard-Tick-Locators (ticker) und Tick-Formatter, die für die Skala geeignet sind. Eine Achse mit einer 'log'-Skala hat einen LogLocator, um Ticks in Zehnerpotenzen-Intervallen auszuwählen, und einen LogFormatter, um die Zehnerpotenzen in wissenschaftlicher Notation darzustellen.

print('X axis')
print(ax.xaxis.get_major_locator())
print(ax.xaxis.get_major_formatter())

print('Y axis')
print(ax.yaxis.get_major_locator())
print(ax.yaxis.get_major_formatter())

X axis
<matplotlib.ticker.AutoLocator object at 0x7315fb20d370>
<matplotlib.ticker.ScalarFormatter object at 0x7315fbfcd5a0>
Y axis
<matplotlib.ticker.LogLocator object at 0x7315faf8f250>
<matplotlib.ticker.LogFormatterSciNotation object at 0x7315fb1e6cd0>