Ein genauerer Blick auf Wahrscheinlichkeitsdiagramme¶

Übersicht¶

Die Funktion probscale.probplot ermöglicht Ihnen einige Dinge. Diese sind:

Erstellung von Perzentil-, Quantil- oder Wahrscheinlichkeitsdiagrammen.
Platzierung Ihrer Wahrscheinlichkeitsskala auf einer beliebigen Achse.
Festlegung einer beliebigen Verteilung für Ihre Wahrscheinlichkeitskala.
Zeichnung einer bestangepassten Linie im linearen Wahrscheinlichkeits- oder logarithmischen Wahrscheinlichkeitsraum.
Berechnung der Plotpositionen Ihrer Daten nach Belieben.
Verwendung von Wahrscheinlichkeitsachsen auf Seaborn FacetGrids

Wir werden all diese Optionen in diesem Tutorial behandeln.

%matplotlib inline

import warnings
warnings.simplefilter('ignore')

import numpy
from matplotlib import pyplot
import seaborn

import probscale
clear_bkgd = {'axes.facecolor':'none', 'figure.facecolor':'none'}
seaborn.set(style='ticks', context='talk', color_codes=True, rc=clear_bkgd)

# load up some example data from the seaborn package
tips = seaborn.load_dataset("tips")
iris = seaborn.load_dataset("iris")

Unterschiedliche Diagrammtypen¶

Im Allgemeinen gibt es drei Diagrammtypen:

Perzentil, auch bekannt als P-P-Diagramme
Quantil, auch bekannt als Q-Q-Diagramme
Wahrscheinlichkeit, auch bekannt als Prob-Diagramme

Perzentildiagramme¶

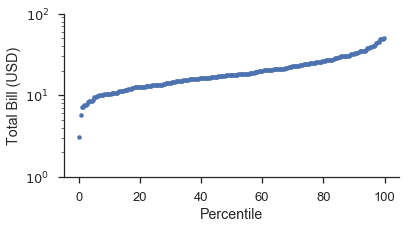
Perzentildiagramme sind die einfachsten Diagramme. Sie zeichnen einfach die Daten gegen ihre Plotpositionen. Die Plotpositionen werden auf einer linearen Skala dargestellt, aber die Daten können entsprechend skaliert werden.

Wenn Sie dies von Grund auf neu machen würden, sähe es so aus:

position, bill = probscale.plot_pos(tips['total_bill'])
position *= 100
fig, ax = pyplot.subplots(figsize=(6, 3))
ax.plot(position, bill, marker='.', linestyle='none', label='Bill amount')
ax.set_xlabel('Percentile')
ax.set_ylabel('Total Bill (USD)')
ax.set_yscale('log')
ax.set_ylim(bottom=1, top=100)
seaborn.despine()

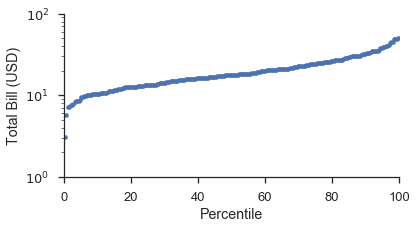
Mit der Funktion probplot und plottype='pp' wird daraus:

fig, ax = pyplot.subplots(figsize=(6, 3))
fig = probscale.probplot(tips['total_bill'], ax=ax, plottype='pp', datascale='log',
                         problabel='Percentile', datalabel='Total Bill (USD)',
                         scatter_kws=dict(marker='.', linestyle='none', label='Bill Amount'))
ax.set_ylim(bottom=1, top=100)
seaborn.despine()

Quantildiagramme¶

Quantildiagramme sind Wahrscheinlichkeitsdiagrammen ähnlich. Die Hauptunterschiede bestehen darin, dass die Plotpositionen in Quantile oder \(Z\)-Werte basierend auf einer Wahrscheinlichkeitsverteilung umgewandelt werden. Die Standardverteilung ist die Standardnormalverteilung. Die Verwendung einer anderen Verteilung wird weiter unten behandelt.

Lassen Sie uns mit demselben Datensatz wie oben ein Quantildiagramm erstellen. Wie oben werden wir es von Grund auf und dann mit probplot machen.

from scipy import stats

position, bill = probscale.plot_pos(tips['total_bill'])
quantile = stats.norm.ppf(position)

fig, ax = pyplot.subplots(figsize=(6, 3))
ax.plot(quantile, bill, marker='.', linestyle='none', label='Bill amount')
ax.set_xlabel('Normal Quantiles')
ax.set_ylabel('Total Bill (USD)')
ax.set_yscale('log')
ax.set_ylim(bottom=1, top=100)
seaborn.despine()

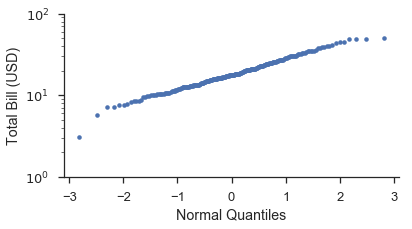
Mit probplot

fig, ax = pyplot.subplots(figsize=(6, 3))
fig = probscale.probplot(tips['total_bill'], ax=ax, plottype='qq', datascale='log',
                         problabel='Standard Normal Quantiles', datalabel='Total Bill (USD)',
                         scatter_kws=dict(marker='.', linestyle='none', label='Bill Amount'))

ax.set_ylim(bottom=1, top=100)
seaborn.despine()

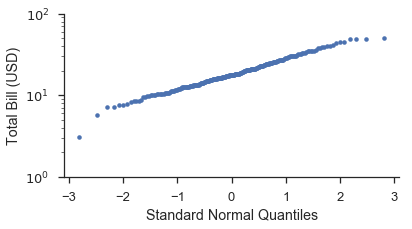
Sie werden feststellen, dass die Form der Daten im Q-Q-Diagramm gerader ist als im P-P-Diagramm. Dies liegt an der Transformation, die stattfindet, wenn die Plotpositionen in die Quantile einer Verteilung umgewandelt werden. Die folgende Grafik veranschaulicht dies hoffentlich deutlicher. Zusätzlich zeigen wir, wie die Option probax verwendet wird, um das Diagramm umzukehren, sodass die P-P/Q-Q/Wahrscheinlichkeitsachse auf der Y-Skala liegt.

fig, (ax1, ax2) = pyplot.subplots(figsize=(6, 6), ncols=2, sharex=True)
markers = dict(marker='.', linestyle='none', label='Bill Amount')

fig = probscale.probplot(tips['total_bill'], ax=ax1, plottype='pp', probax='y',
                         datascale='log', problabel='Percentiles',
                         datalabel='Total Bill (USD)', scatter_kws=markers)

fig = probscale.probplot(tips['total_bill'], ax=ax2, plottype='qq', probax='y',
                         datascale='log', problabel='Standard Normal Quantiles',
                         datalabel='Total Bill (USD)', scatter_kws=markers)

ax1.set_xlim(left=1, right=100)
fig.tight_layout()
seaborn.despine()

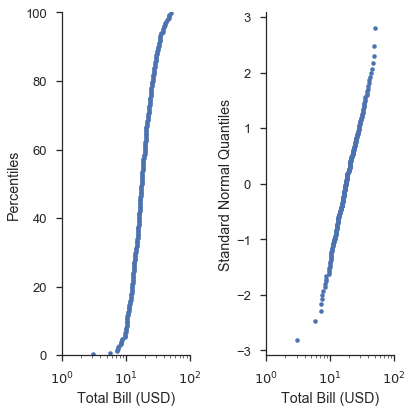
In den Fällen von P-P-Diagrammen und einfachen Q-Q-Diagrammen bietet die Funktion probplot nicht viel Komfort im Vergleich zur Erstellung von rohen Matplotlib-Befehlen. Dies ändert sich jedoch, wenn Sie Wahrscheinlichkeitsdiagramme erstellen und erweiterte Optionen verwenden.

Wahrscheinlichkeitsdiagramme¶

Visuell sollten die Kurven in Wahrscheinlichkeits- und Quantilskalen gleich sein. Der Unterschied besteht darin, dass die Achsenmarkierungen und -beschriftungen basierend auf Wahrscheinlichkeiten der Nicht-Überschreitung platziert und beschriftet werden, anstatt auf den abstrakteren Quantilen der Verteilung.

Wenig überraschend erklärt ein Bild dies viel besser. Lassen Sie uns auf dem vorherigen Diagramm aufbauen.

fig, (ax1, ax2, ax3) = pyplot.subplots(figsize=(9, 6), ncols=3, sharex=True)
common_opts = dict(
    probax='y',
    datascale='log',
    datalabel='Total Bill (USD)',
    scatter_kws=dict(marker='.', linestyle='none')
)

fig = probscale.probplot(tips['total_bill'], ax=ax1, plottype='pp',
                         problabel='Percentiles',  **common_opts)

fig = probscale.probplot(tips['total_bill'], ax=ax2, plottype='qq',
                         problabel='Standard Normal Quantiles',  **common_opts)

fig = probscale.probplot(tips['total_bill'], ax=ax3, plottype='prob',
                         problabel='Standard Normal Probabilities',  **common_opts)

ax3.set_xlim(left=1, right=100)
ax3.set_ylim(bottom=0.13, top=99.87)
fig.tight_layout()
seaborn.despine()

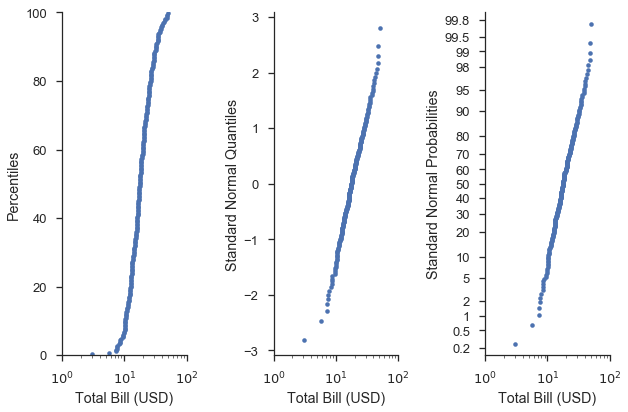
Visuell sind die Formen der Kurven in den rechtesten Diagrammen identisch. Der Unterschied besteht darin, dass die Y-Achsenmarkierungen und -beschriftungen "menschenlesbarer" sind.

Mit anderen Worten, die Wahrscheinlichkeit (rechte) Achse gibt uns die Leichtigkeit, z. B. das 75. Perzentil auf der Perzentil- (linke) Achse zu finden, und veranschaulicht, wie gut die Daten zu einer gegebenen Verteilung passen, ähnlich wie die Quantil- (mittlere) Achsen.

Verwendung unterschiedlicher Verteilungen für Ihre Skalen¶

Bei der Verwendung von Quantil- oder Wahrscheinlichkeitskalen können Sie eine Verteilung aus dem scipy.stats-Modul an die Funktion probplot übergeben. Wenn dem Parameter dist keine Verteilung übergeben wird, wird eine Standardnormalverteilung verwendet.

common_opts = dict(
    plottype='prob',
    probax='y',
    datascale='log',
    datalabel='Total Bill (USD)',
    scatter_kws=dict(marker='+', linestyle='none', mew=1)
)

alpha = stats.alpha(10)
beta = stats.beta(6, 3)

fig, (ax1, ax2, ax3) = pyplot.subplots(figsize=(9, 6), ncols=3, sharex=True)
fig = probscale.probplot(tips['total_bill'], ax=ax1, dist=alpha,
                         problabel='Alpha(10) Probabilities', **common_opts)

fig = probscale.probplot(tips['total_bill'], ax=ax2, dist=beta,
                         problabel='Beta(6, 1) Probabilities', **common_opts)

fig = probscale.probplot(tips['total_bill'], ax=ax3, dist=None,
                         problabel='Standard Normal Probabilities', **common_opts)

ax3.set_xlim(left=1, right=100)
for ax in [ax1, ax2, ax3]:
    ax.set_ylim(bottom=0.2, top=99.8)
seaborn.despine()
fig.tight_layout()

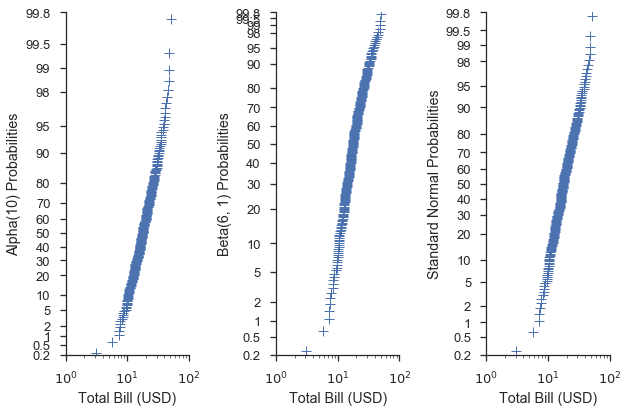
Dies kann auch für QQ-Skalen erfolgen.

common_opts = dict(
    plottype='qq',
    probax='y',
    datascale='log',
    datalabel='Total Bill (USD)',
    scatter_kws=dict(marker='+', linestyle='none', mew=1)
)

alpha = stats.alpha(10)
beta = stats.beta(6, 3)

fig, (ax1, ax2, ax3) = pyplot.subplots(figsize=(9, 6), ncols=3, sharex=True)
fig = probscale.probplot(tips['total_bill'], ax=ax1, dist=alpha,
                         problabel='Alpha(10) Quantiles', **common_opts)

fig = probscale.probplot(tips['total_bill'], ax=ax2, dist=beta,
                         problabel='Beta(6, 3) Quantiles', **common_opts)

fig = probscale.probplot(tips['total_bill'], ax=ax3, dist=None,
                         problabel='Standard Normal Quantiles', **common_opts)

ax1.set_xlim(left=1, right=100)
seaborn.despine()
fig.tight_layout()

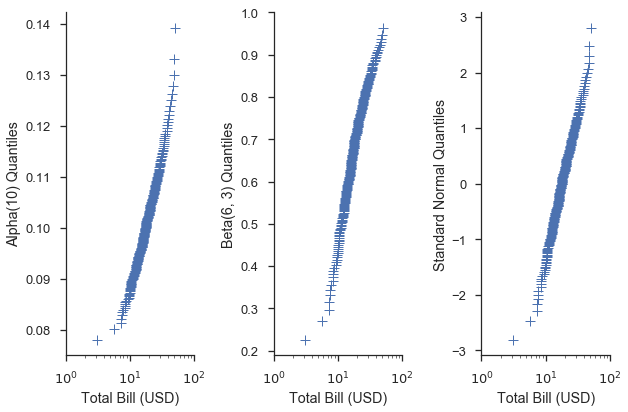
Die Verwendung einer bestimmten Verteilung mit einer Quantilskala kann uns eine Vorstellung davon geben, wie gut die Daten zu dieser Verteilung passen. Angenommen, wir haben beispielsweise die Ahnung, dass die Werte der Spalte total_bill in unserem Datensatz normalverteilt sind und ihre Mittelwerte und Standardabweichungen 19,8 bzw. 8,9 betragen. Wir könnten dies untersuchen, indem wir eine scipy.stat.norm-Verteilung mit diesen Parametern erstellen und diese Verteilung im Q-Q-Diagramm verwenden.

def equality_line(ax, label=None):
    limits = [
        numpy.min([ax.get_xlim(), ax.get_ylim()]),
        numpy.max([ax.get_xlim(), ax.get_ylim()]),
    ]
    ax.set_xlim(limits)
    ax.set_ylim(limits)
    ax.plot(limits, limits, 'k-', alpha=0.75, zorder=0, label=label)

norm = stats.norm(loc=21, scale=8)
fig, ax = pyplot.subplots(figsize=(5, 5))
ax.set_aspect('equal')

common_opts = dict(
    plottype='qq',
    probax='x',
    problabel='Theoretical Quantiles',
    datalabel='Emperical Quantiles',
    scatter_kws=dict(label='Bill amounts')
)

fig = probscale.probplot(tips['total_bill'], ax=ax, dist=norm, **common_opts)

equality_line(ax, label='Guessed Normal Distribution')
ax.legend(loc='lower right')
seaborn.despine()

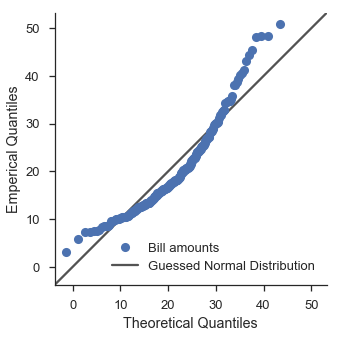
Hm. Das sieht nicht sehr gut aus. Verwenden wir die Fitting-Funktionalität von Scipy, um eine Lognormalverteilung auszuprobieren.

lognorm_params = stats.lognorm.fit(tips['total_bill'], floc=0)
lognorm = stats.lognorm(*lognorm_params)
fig, ax = pyplot.subplots(figsize=(5, 5))
ax.set_aspect('equal')

fig = probscale.probplot(tips['total_bill'], ax=ax, dist=lognorm, **common_opts)

equality_line(ax, label='Fit Lognormal Distribution')
ax.legend(loc='lower right')
seaborn.despine()

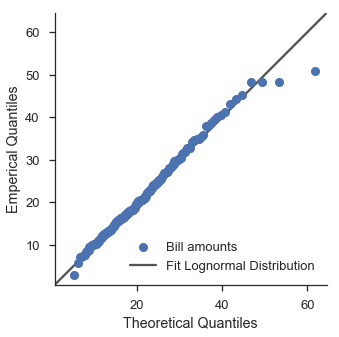
Das ist schon etwas besser.

Das Finden der besten Verteilung wird dem Leser als Übung überlassen.

Bestangepasste Linien¶

Das Hinzufügen einer bestangepassten Linie zu einem Wahrscheinlichkeitsdiagramm kann Aufschluss darüber geben, ob ein Datensatz durch eine bestimmte Verteilung charakterisiert werden kann oder nicht.

Dies geschieht einfach mit der Option bestfit=True in probplot. Intern transformiert probplot sowohl die X- als auch die Y-Daten, die der Regression zugeführt werden, basierend auf dem Diagrammtyp und der Skala der Datenachse (gesteuert über datascale).

Visuelle Attribute der Linie können mit dem Parameter line_kws gesteuert werden. Wenn Sie die bestangepasste Linie beschriften möchten, geben Sie hier deren Beschriftung an.

Einfache Beispiele¶

Der trivialste Fall ist ein P-P-Diagramm mit einer linearen Datenachse.

fig, ax = pyplot.subplots(figsize=(6, 3))
fig = probscale.probplot(tips['total_bill'], ax=ax, plottype='pp', bestfit=True,
                         problabel='Percentile', datalabel='Total Bill (USD)',
                         scatter_kws=dict(label='Bill Amount'),
                         line_kws=dict(label='Best-fit line'))
ax.legend(loc='upper left')
seaborn.despine()

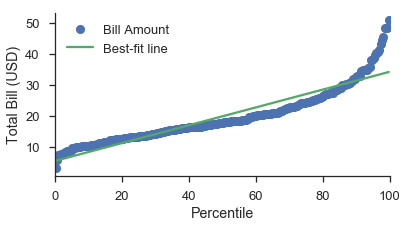
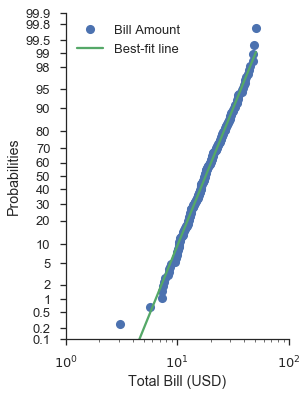
Der am wenigsten triviale Fall ist ein Wahrscheinlichkeitsdiagramm mit einer logarithmisch skalierten Datenachse.

Wie im Abschnitt über Quantildiagramme mit benutzerdefinierten Verteilungen vorgeschlagen, bietet die Verwendung einer normalen Wahrscheinlichkeitskala mit einer lognormalen Datenskala eine anständige Passung (visuell gesprochen).

Beachten Sie, dass Sie die Wahrscheinlichkeitskala weiterhin auf entweder die X- oder die Y-Achse legen.

fig, ax = pyplot.subplots(figsize=(4, 6))
fig = probscale.probplot(tips['total_bill'], ax=ax, plottype='prob', probax='y', bestfit=True,
                         datascale='log', problabel='Probabilities', datalabel='Total Bill (USD)',
                         scatter_kws=dict(label='Bill Amount'),
                         line_kws=dict(label='Best-fit line'))
ax.legend(loc='upper left')
ax.set_ylim(bottom=0.1, top=99.9)
ax.set_xlim(left=1, right=100)
seaborn.despine()

Bootstrapped Konfidenzintervalle¶

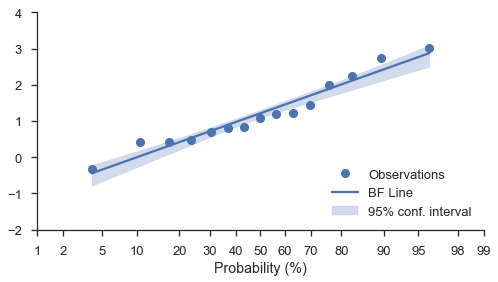
Unabhängig von den Skalen des Diagramms (linear, log oder prob) können Sie bootstrapped Konfidenzintervalle um die bestangepasste Linie hinzufügen. Verwenden Sie einfach die Option estimate_ci=True zusammen mit bestfit=True

N = 15
numpy.random.seed(0)
x = numpy.random.normal(size=N) + numpy.random.uniform(size=N)
fig, ax = pyplot.subplots(figsize=(8, 4))
fig = probscale.probplot(x, ax=ax, bestfit=True, estimate_ci=True,
                         line_kws={'label': 'BF Line', 'color': 'b'},
                         scatter_kws={'label': 'Observations'},
                         problabel='Probability (%)')
ax.legend(loc='lower right')
ax.set_ylim(bottom=-2, top=4)
seaborn.despine(fig)

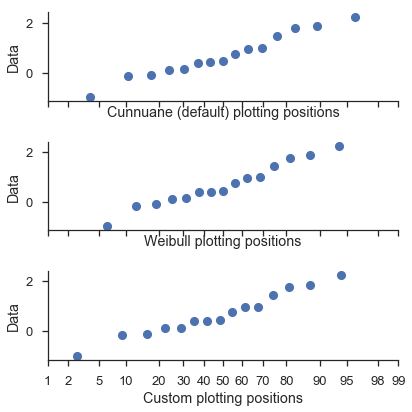
Anpassen der Plotpositionen¶

Die Funktion probplot ruft die Funktion viz.plot_plos() auf, um die Plotpositionen jedes Datensatzes zu berechnen.

Lesen Sie die Docstrings dieser Funktion für detailliertere Informationen. Aber der High-Level-Überblick ist, dass es ein paar Parameter (alpha und beta) gibt, die Sie bei der Berechnung der Plotpositionen anpassen können.

Die gebräuchlichsten Werte können über den Parameter postype ausgewählt werden.

Diese werden über den Parameter pp_kws in probplot gesteuert und im nächsten Tutorial ausführlicher behandelt.

common_opts = dict(
    plottype='prob',
    probax='x',
    datalabel='Data',
)

numpy.random.seed(0)
x = numpy.random.normal(size=15)

fig, (ax1, ax2, ax3) = pyplot.subplots(figsize=(6, 6), nrows=3,
                                       sharey=True, sharex=True)
fig = probscale.probplot(x, ax=ax1, problabel='Cunnuane (default) plotting positions',
                         **common_opts)

fig = probscale.probplot(x, ax=ax2, problabel='Weibull plotting positions',
                         pp_kws=dict(postype='weibull'), **common_opts)

fig = probscale.probplot(x, ax=ax3, problabel='Custom plotting positions',
                         pp_kws=dict(alpha=0.6, beta=0.1), **common_opts)
ax1.set_xlim(left=1, right=99)
seaborn.despine()
fig.tight_layout()

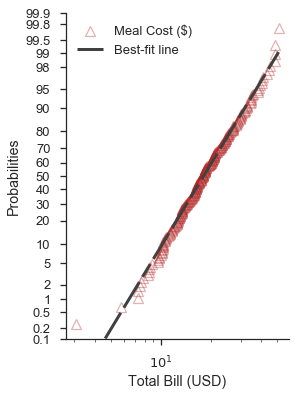
Steuerung der Ästhetik der Plot-Elemente¶

Wie in den obigen Beispielen angedeutet, nimmt die Funktion probplot zwei Wörterbücher entgegen, um die Datenreihen und die bestangepasste Linie anzupassen (scatter_kws und line_kws, bzw. die zugehörige Linie). Diese Wörterbücher werden direkt an die Methode plot der aktuellen Achsen übergeben.

Standardmäßig geht die Datenreihe davon aus, dass linestyle='none' und marker='o' sind. Diese können über scatter_kws überschrieben werden.

Wenn wir das vorherige Beispiel noch einmal durchgehen, können wir es wie folgt anpassen:

scatter_options = dict(
    marker='^',
    markerfacecolor='none',
    markeredgecolor='firebrick',
    markeredgewidth=1.25,
    linestyle='none',
    alpha=0.35,
    zorder=5,
    label='Meal Cost ($)'
)

line_options = dict(
    dashes=(10,2,5,2,10,2),
    color='0.25',
    linewidth=3,
    zorder=10,
    label='Best-fit line'
)

fig, ax = pyplot.subplots(figsize=(4, 6))
fig = probscale.probplot(tips['total_bill'], ax=ax, plottype='prob', probax='y', bestfit=True,
                         datascale='log', problabel='Probabilities', datalabel='Total Bill (USD)',
                         scatter_kws=scatter_options, line_kws=line_options)
ax.legend(loc='upper left')
ax.set_ylim(bottom=0.1, top=99.9)
seaborn.despine()

Hinweis

Die Funktion probplot kann zwei zusätzliche ästhetische Parameter annehmen: color und label. Wenn angegeben, überschreibt color die Optionen für die Marker-Füllfarbe und die Linienfarbe der Parameter scatter_kws und line_kws entsprechend. Ebenso wird die Beschriftung der Scatter-Reihe durch den expliziten Parameter überschrieben. Es wird nicht empfohlen, color und label zu verwenden. Sie existieren hauptsächlich zur Kompatibilität mit dem Seaborn-Paket.

Abbildung von Wahrscheinlichkeitsdiagrammen auf Seaborn FacetGrids ¶

Im Allgemeinen wurde probplot mit FacetGrids im Sinn geschrieben. Alles, was Sie tun müssen, ist, die Datenspalte und andere Optionen im Aufruf von FacetGrid.map anzugeben.

Leider funktionieren die Beschriftungen nicht ganz wie gewünscht, aber es ist ein fortlaufendes Projekt.

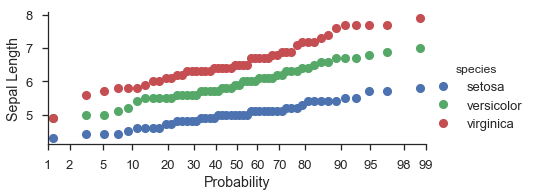
fg = (
    seaborn.FacetGrid(data=iris, hue='species', aspect=2)
        .map(probscale.probplot, 'sepal_length')
        .set_axis_labels(x_var='Probability', y_var='Sepal Length')
        .add_legend()
)

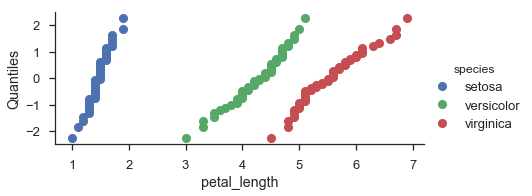
fg = (
    seaborn.FacetGrid(data=iris, hue='species', aspect=2)
        .map(probscale.probplot, 'petal_length', plottype='qq', probax='y')
        .set_ylabels('Quantiles')
        .add_legend()
)

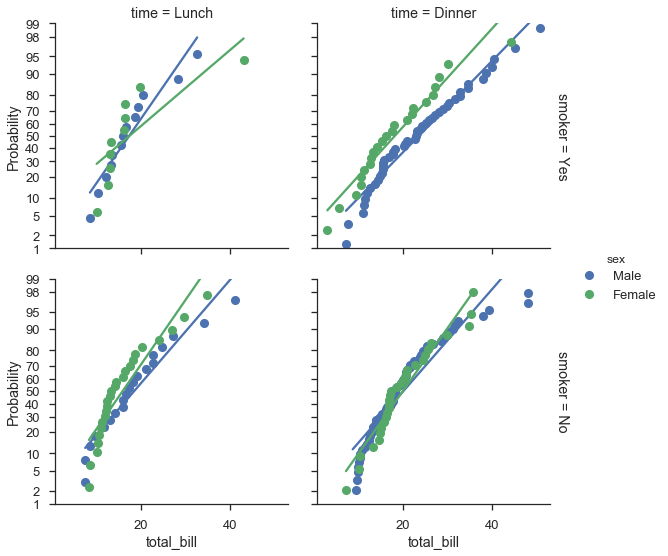
fg = (
    seaborn.FacetGrid(data=tips, hue='sex', row='smoker', col='time', margin_titles=True, size=4)
        .map(probscale.probplot, 'total_bill', probax='y', bestfit=True)
        .set_ylabels('Probability')
        .add_legend()
)