Verwendung unterschiedlicher Formulierungen von Plotting-Positionen¶
Berechnung von Plotting-Positionen¶
Beim Erstellen eines Perzentil-, Quantil- oder Wahrscheinlichkeitsdiagramms müssen die Plotting-Positionen der geordneten Daten berechnet werden.
Für eine Stichprobe \(X\) mit Populationsgröße \(n\) ist die Plotting-Position des \(j^\mathrm{th}\)-Elements definiert als
In dieser Gleichung können α und β verschiedene Werte annehmen. Gängige Werte werden unten beschrieben
- „Typ 4“ (α=0, β=1)
- Lineare Interpolation der empirischen CDF.
- „Typ 5“ oder „Hazen“ (α=0,5, β=0,5)
- Stückweise lineare Interpolation.
- „Typ 6“ oder „Weibull“ (α=0, β=0)
- Weibull-Plotting-Positionen. Erwartungswertfreie Überschreitungswahrscheinlichkeit für alle Verteilungen. Empfohlen für hydrologische Anwendungen.
- „Typ 7“ (α=1, β=1)
- Die Standardwerte in R. Nicht empfohlen mit Wahrscheinlichkeitsskalen, da die minimalen und maximalen Datenpunkte Plotting-Positionen von 0 bzw. 1 erhalten und daher nicht angezeigt werden können.
- „Typ 8“ (α=1/3, β=1/3)
- Ungefähr median-erwartungswertfrei.
- „Typ 9“ oder „Blom“ (α=0,375, β=0,375)
- Ungefähr erwartungswertfreie Positionen, wenn die Daten normalverteilt sind.
- „Median“ (α=0,3175, β=0,3175)
- Median-Überschreitungswahrscheinlichkeiten für alle Verteilungen (verwendet in
scipy.stats.probplot).- „apl“ oder „pwm“ (α=0,35, β=0,35)
- Verwendet mit wahrscheinkeitsgewichteten Momenten.
- „Cunnane“ (α=0,4, β=0,4)
- Nahezu erwartungswertfreie Quantile für normalverteilte Daten. Dies ist der Standardwert.
- „Gringorten“ (α=0,44, β=0,44)
- Verwendet für Gumbel-Verteilungen.
Der Zweck dieses Tutorials ist es zu zeigen, wie die ausgewählten α und β die Form eines Wahrscheinlichkeitsdiagramms verändern können.
Lassen Sie uns zuerst einige analytische Grundlagen klären...
%matplotlib inline
import warnings
warnings.simplefilter('ignore')
import numpy
from matplotlib import pyplot
from scipy import stats
import seaborn
clear_bkgd = {'axes.facecolor':'none', 'figure.facecolor':'none'}
seaborn.set(style='ticks', context='talk', color_codes=True, rc=clear_bkgd)
import probscale
def format_axes(ax1, ax2):
""" Sets axes labels and grids """
for ax in (ax1, ax2):
if ax is not None:
ax.set_ylim(bottom=1, top=99)
ax.set_xlabel('Values of Data')
seaborn.despine(ax=ax)
ax.yaxis.grid(True)
ax1.legend(loc='upper left', numpoints=1, frameon=False)
ax1.set_ylabel('Normal Probability Scale')
if ax2 is not None:
ax2.set_ylabel('Weibull Probability Scale')
Normale vs. Weibull-Skalen und Cunnane vs. Weibull-Plotting-Positionen¶
Hier generieren wir einige gefälschte, normalverteilte Daten und definieren eine Weibull-Verteilung aus scipy, die wir für eine Wahrscheinlichkeitsskala verwenden werden.
numpy.random.seed(0) # reproducible
data = numpy.random.normal(loc=5, scale=1.25, size=37)
# simple weibull distribution
weibull = stats.weibull_min(2)
Nun erstellen wir Wahrscheinlichkeitsdiagramme auf sowohl Weibull- als auch normalen Wahrscheinlichkeitsskalen. Zusätzlich berechnen wir die Plotting-Positionen auf zwei verschiedene, aber übliche Weisen für jedes Diagramm.
Zuerst zeigen wir in blauen Kreisen die Daten mit Weibull- (α=0, β=0) Plotting-Positionen. Weibull-Plotting-Positionen werden häufig in Bereichen wie Hydrologie und Wasserressourcen-Ingenieurwesen verwendet.
In grünen Quadraten verwenden wir Cunnane- (α=0,4, β=0,4) Plotting-Positionen. Cunnane-Plotting-Positionen eignen sich gut für normalverteilte Daten und sind die Standardwerte.
w_opts = {'label': 'Weibull (α=0, β=0)', 'marker': 'o', 'markeredgecolor': 'b'}
c_opts = {'label': 'Cunnane (α=0.4, β=0.4)', 'marker': 's', 'markeredgecolor': 'g'}
common_opts = {
'markerfacecolor': 'none',
'markeredgewidth': 1.25,
'linestyle': 'none'
}
fig, (ax1, ax2) = pyplot.subplots(figsize=(10, 8), ncols=2, sharex=True, sharey=False)
for dist, ax in zip([None, weibull], [ax1, ax2]):
for opts, postype in zip([w_opts, c_opts,], ['weibull', 'cunnane']):
probscale.probplot(data, ax=ax, dist=dist, probax='y',
scatter_kws={**opts, **common_opts},
pp_kws={'postype': postype})
format_axes(ax1, ax2)
fig.tight_layout()
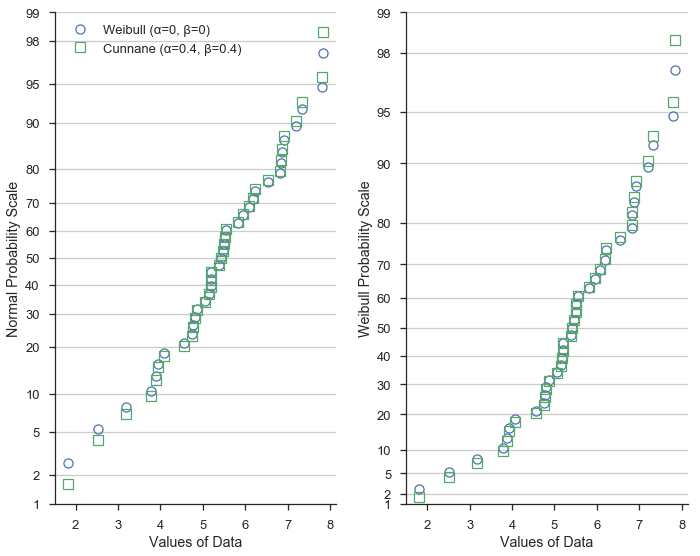
Dies zeigt, dass die verschiedenen Formulierungen der Plotting-Positionen sich am stärksten an den extremen Werten des Datensatzes unterscheiden.
Hazen-Plotting-Positionen¶
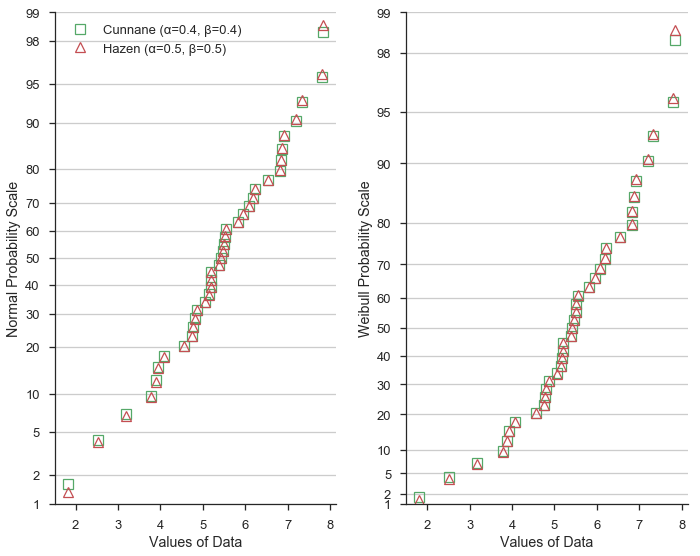
Als nächstes vergleichen wir die Hazen/Typ 5 (α=0,5, β=0,5) Formulierung mit Cunnane. Hazen-Plotting-Positionen (dargestellt als rote Dreiecke) repräsentieren eine stückweise lineare Interpolation der empirischen kumulativen Verteilungsfunktion des Datensatzes.
Da die Werte von α=0,5 und β=0,5 nur geringfügig von den Cunnane-Werten abweichen, sind die Plotting-Positionen erwartungsgemäß ähnlich.
h_opts = {'label': 'Hazen (α=0.5, β=0.5)', 'marker': '^', 'markeredgecolor': 'r'}
fig, (ax1, ax2) = pyplot.subplots(figsize=(10, 8), ncols=2, sharex=True, sharey=False)
for dist, ax in zip([None, weibull], [ax1, ax2]):
for opts, postype in zip([c_opts, h_opts,], ['cunnane', 'Hazen']):
probscale.probplot(data, ax=ax, dist=dist, probax='y',
scatter_kws={**opts, **common_opts},
pp_kws={'postype': postype})
format_axes(ax1, ax2)
fig.tight_layout()
Zusammenfassung¶
Auf die Gefahr hin, eine sehr unübersichtliche und schwer lesbare Abbildung zu zeigen, werfen wir alle drei auf dieselbe normale Wahrscheinlichkeitsskala.
fig, ax1 = pyplot.subplots(figsize=(6, 8))
for opts, postype in zip([w_opts, c_opts, h_opts,], ['weibull', 'cunnane', 'hazen']):
probscale.probplot(data, ax=ax1, dist=None, probax='y',
scatter_kws={**opts, **common_opts},
pp_kws={'postype': postype})
format_axes(ax1, None)
fig.tight_layout()
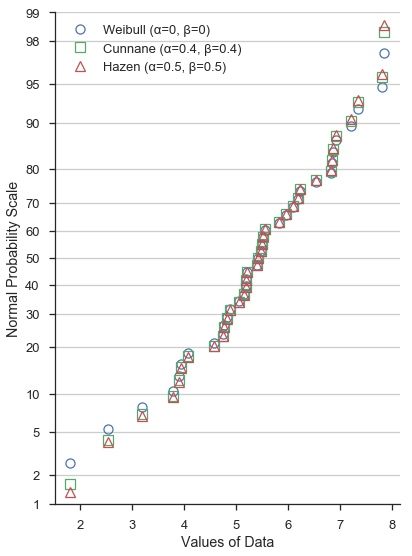
Auch hier verändern die unterschiedlichen Werte von α und β die Form des Wahrscheinlichkeitsdiagramms in der Regel nicht wesentlich zwischen – sagen wir – dem unteren und oberen Quartil. Außerhalb der Quartile ist der Unterschied jedoch offensichtlicher.
Die folgende Zelle berechnet die Plotting-Positionen mit den drei untersuchten α- und β-Werten und gibt die ersten zehn Werte zum einfachen Vergleich aus.
# weibull plotting positions and sorted data
w_probs, _ = probscale.plot_pos(data, postype='weibull')
# normal plotting positions, returned "data" is identical to above
c_probs, _ = probscale.plot_pos(data, postype='cunnane')
# type 4 plot positions
h_probs, _ = probscale.plot_pos(data, postype='hazen')
# convert to percentages
w_probs *= 100
c_probs *= 100
h_probs *= 100
print('Weibull: ', numpy.round(w_probs[:10], 2))
print('Cunnane: ', numpy.round(c_probs[:10], 2))
print('Hazen: ', numpy.round(h_probs[:10], 2))
Weibull: [ 2.63 5.26 7.89 10.53 13.16 15.79 18.42 21.05 23.68 26.32]
Cunnane: [ 1.61 4.3 6.99 9.68 12.37 15.05 17.74 20.43 23.12 25.81]
Hazen: [ 1.35 4.05 6.76 9.46 12.16 14.86 17.57 20.27 22.97 25.68]